Working Directory
Manually Enter Data
dat <- data.frame(X = c(4.1, 5.2, 7.5, 8.2, 9.3, 3.1, 1.6,
6.0, 7.4, 6.5, 5.1, 9.6, 2.8, 5.9),
Y = c(15.1, 11.2, 22.5, 25.4, 26.0, 10.5, 9.9,
17.7, 19.9, 16.5, 14.3, 30.2, 9.7, 15.7))
colnames(dat) <- c("June1234", "June5678") # change the variable name
dat # view the data
June1234 June5678
1 4.1 15.1
2 5.2 11.2
3 7.5 22.5
4 8.2 25.4
5 9.3 26.0
6 3.1 10.5
7 1.6 9.9
8 6.0 17.7
9 7.4 19.9
10 6.5 16.5
11 5.1 14.3
12 9.6 30.2
13 2.8 9.7
14 5.9 15.7
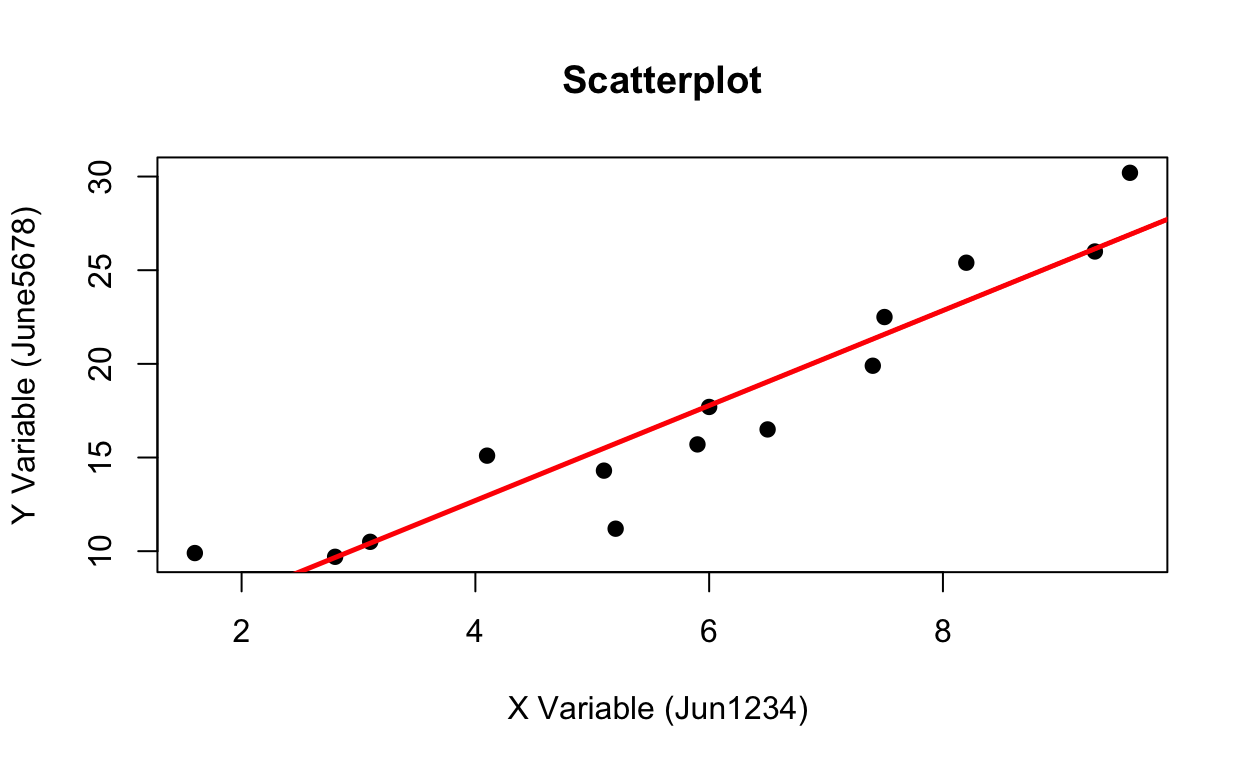
Scatterplot
plot(x = dat$June1234, y = dat$June5678, main="Scatterplot",
xlab = "X Variable (Jun1234) ", ylab = "Y Variable (June5678)", pch = 19)
# add a regression fit line
plot(x = dat$June1234,
y = dat$June5678,
main="Scatterplot",
xlab = "X Variable (Jun1234) ",
ylab = "Y Variable (June5678)", pch = 19)
abline(lm(dat$June5678 ~ dat$June1234), col="red", lwd = 2.5)
Correlation
Pearson's product-moment correlation
data: June1234 and June5678
t = 9.4868, df = 12, p-value = 6.309e-07
alternative hypothesis: true correlation is not equal to 0
95 percent confidence interval:
0.8148934 0.9809951
sample estimates:
cor
0.9393361
Regression
rfit <- lm(dat$June5678 ~ dat$June1234)
summary(rfit)
Call:
lm(formula = dat$June5678 ~ dat$June1234)
Residuals:
Min 1Q Median 3Q Max
-4.5503 -1.3719 -0.0213 1.7595 3.2898
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.5614 1.6906 1.515 0.156
dat$June1234 2.5363 0.2674 9.487 6.31e-07 ***
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 2.331 on 12 degrees of freedom
Multiple R-squared: 0.8824, Adjusted R-squared: 0.8725
F-statistic: 90 on 1 and 12 DF, p-value: 6.309e-07
