EDMS 657-R Tutorial: Principal Components Analysis
Yi Feng & Gregory R. Hancock
University of Maryland, College ParkIn this document we demonstrate some simple examples of principal components analysis using R. This document serves as a supplementary material for EDMS 657-Exploratory Latent and Composite Variable Methods, taught by Dr. Gregory R. Hancock at University of Maryland.
Before we get started, let’s make sure we install and load all the packages we need to use in this demo.
install.packages("FactoMinR")
install.packages("factoextra")
install.packages("foreign")
install.packages("scatterplot3d")
install.packages("corrplot")
install.packages("nFactors")
install.packages("GPArotation")
install.packages("tidyverse")library(FactoMineR)
library(factoextra)
library(foreign)
library(scatterplot3d)
library(corrplot)
library(psych)
library(nFactors)
library(GPArotation)
library(EDMS657Data)
library(tidyverse)Example 1: PCA with a correlation matrix for two observed variables
1. Prepare data
(data <- matrix(c(1, 0.724,
0.724, 1), byrow = T, nrow = 2))## [,1] [,2]
## [1,] 1.000 0.724
## [2,] 0.724 1.0002. Perform PCA on the correlation matrix
Here you can use the principal() function in the
existing R package psych:
(pca1 <- principal(data, nfactors = 1)) # extract only 1 component## Principal Components Analysis
## Call: principal(r = data, nfactors = 1)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 h2 u2 com
## 1 0.93 0.86 0.14 1
## 2 0.93 0.86 0.14 1
##
## PC1
## SS loadings 1.72
## Proportion Var 0.86
##
## Mean item complexity = 1
## Test of the hypothesis that 1 component is sufficient.
##
## The root mean square of the residuals (RMSR) is 0.14
##
## Fit based upon off diagonal values = 0.96(pca2 <- principal(data, nfactors = 2, rotate = 'none')) # extract 2 components## Principal Components Analysis
## Call: principal(r = data, nfactors = 2, rotate = "none")
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 h2 u2 com
## 1 0.93 -0.37 1 2.2e-16 1.3
## 2 0.93 0.37 1 2.2e-16 1.3
##
## PC1 PC2
## SS loadings 1.72 0.28
## Proportion Var 0.86 0.14
## Cumulative Var 0.86 1.00
## Proportion Explained 0.86 0.14
## Cumulative Proportion 0.86 1.00
##
## Mean item complexity = 1.3
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0
##
## Fit based upon off diagonal values = 1See the scree plot:
VSS.scree(data)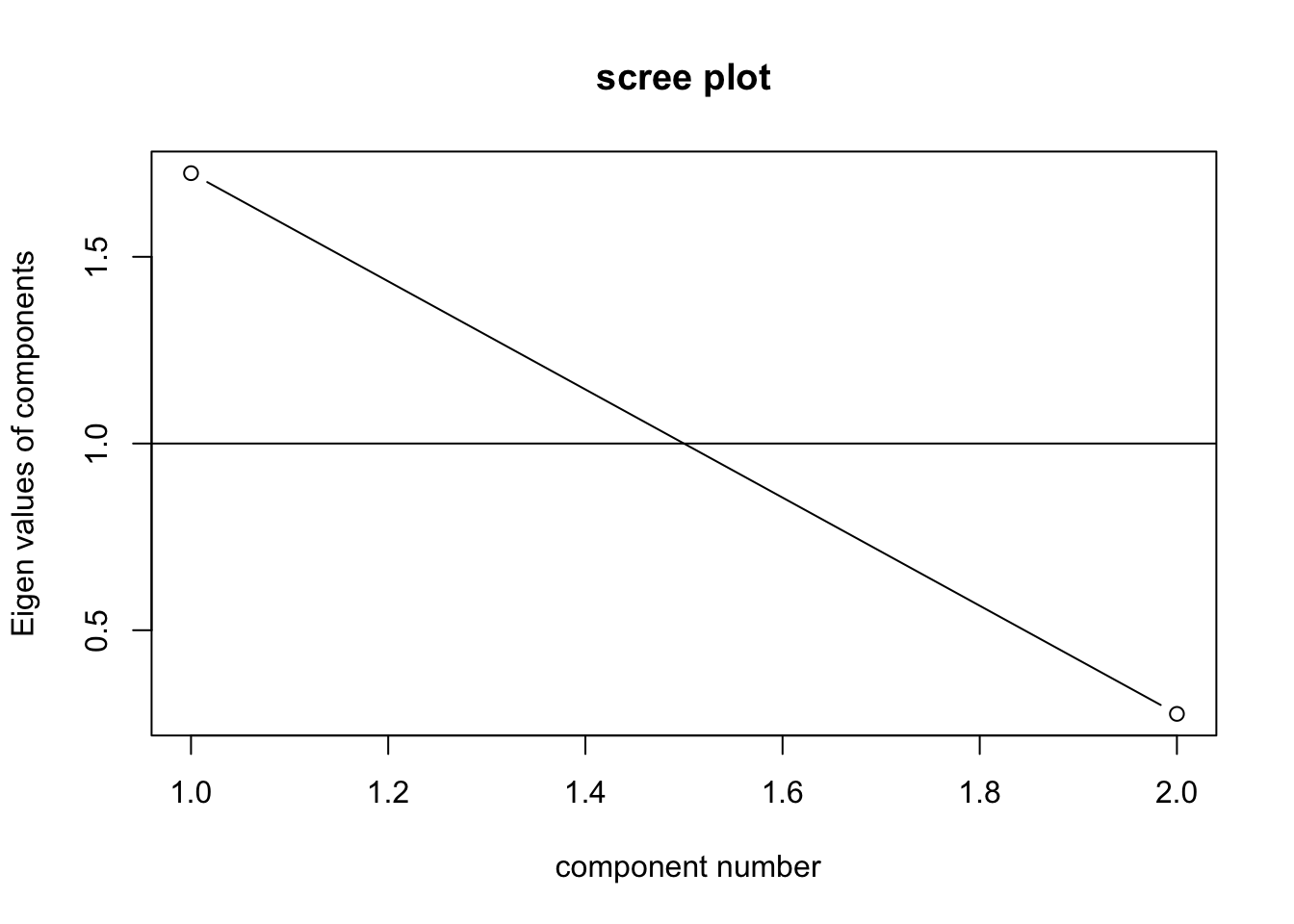
3. An alternative approach if you want some more fun. :)
Alternatively, you can choose to do it manually. First, you start with the eigendecomposition of the correlation matrix:
\[ \begin{aligned} \mathbf{S}=\mathbf{Q\Lambda Q}^{-1}, \end{aligned} \]
where \(\mathbf{S}\) is the sample correlation matrix, \(\mathbf{Q}\) is a matrix of eigenvectors for \(\mathbf{S}\), and \(\mathbf{\Lambda}\) contains the corresponding eigenvalues for the eigenvectors. Eigenvectors and values come in pairs. Every eigenvector has a corresponding eigenvalue. In brief, eigenvectors tell you the direction of the principal components, and eigenvlues tell you how much the data vary in that specific direction. Eigenvectors usually have unit length and they are linearly independent of one another.
For standardized variables, the (unrotated) factor loadings are given by
\[ \begin{aligned} \mathbf{L}=\mathbf{Q}\sqrt{\mathbf{\Lambda}} \end{aligned} \]
which tell you the correlations between the original variables \(\mathbf{X}\) and the (unrotated) principal components \(\mathbf{Z}\).
For \(j^{\text{th}}\) principal component, the corresponding eigenvalue can be computed as the sum of squared loadings across the \(k\) variables.
\[ \begin{aligned} \sum_{i=1}^{k}l_{ij}^2 \end{aligned} \] or \[ \mathbf{l}_j^{'}\mathbf{l}_j \]
# eigendecomposition
(eign <- eigen(data))## eigen() decomposition
## $values
## [1] 1.724 0.276
##
## $vectors
## [,1] [,2]
## [1,] 0.7071068 -0.7071068
## [2,] 0.7071068 0.7071068(eigenval <- diag(eign$values,nrow=2,ncol=2))## [,1] [,2]
## [1,] 1.724 0.000
## [2,] 0.000 0.276# get the loadings
load <- eign$vectors%*%sqrt(eigenval)
colnames(load) <- c("PC1", "PC2")
rownames(load) <- c("X1", "X2")
load ## PC1 PC2
## X1 0.9284396 -0.3714835
## X2 0.9284396 0.3714835# percent var explained
colSums(load^2)/2## PC1 PC2
## 0.862 0.138diag(t(load)%*%load)/nrow(load)## PC1 PC2
## 0.862 0.138# compute the communality
load[,1]^2## X1 X2
## 0.862 0.862rowSums(load^2)## X1 X2
## 1 1diag(load%*%t(load))## X1 X2
## 1 1You can check the properties of eigendecomposition. For example, you can confirm the unit length of eigen vectors and their linear independence.
t(eign$vectors)%*%eign$vectors## [,1] [,2]
## [1,] 1 0
## [2,] 0 1You can reconstruct the correlation matrix:
data.cor <- eign$vectors%*%eigenval%*%t(eign$vectors)
colnames(data.cor) <- rownames(data.cor) <- c("X1", "X2")
data.cor## X1 X2
## X1 1.000 0.724
## X2 0.724 1.000You can recover the eigenvalues from the loadings:
colSums(load^2)## PC1 PC2
## 1.724 0.276diag(t(load)%*%load)## PC1 PC2
## 1.724 0.276Example 2: PCA for data reduction with the female turtles data
1. Read data and explore the data
library(EDMS657Data)
describe(turtle)## vars n mean sd median trimmed mad min max range skew
## length 1 24 134.23 21.35 134.20 135.10 17.59 84.58 168.13 83.55 -0.35
## width 2 24 101.76 13.12 101.84 102.00 13.95 74.66 124.19 49.53 -0.27
## height 3 24 51.35 8.17 51.66 51.58 7.65 35.65 65.31 29.66 -0.27
## kurtosis se
## length -0.41 4.36
## width -0.74 2.68
## height -0.73 1.67(turtle.cor <- cor(turtle))## length width height
## length 1.0000000 0.9751657 0.9713867
## width 0.9751657 1.0000000 0.9654016
## height 0.9713867 0.9654016 1.0000000# visualize the data
scatterplot3d(turtle, pch = 16, color="steelblue")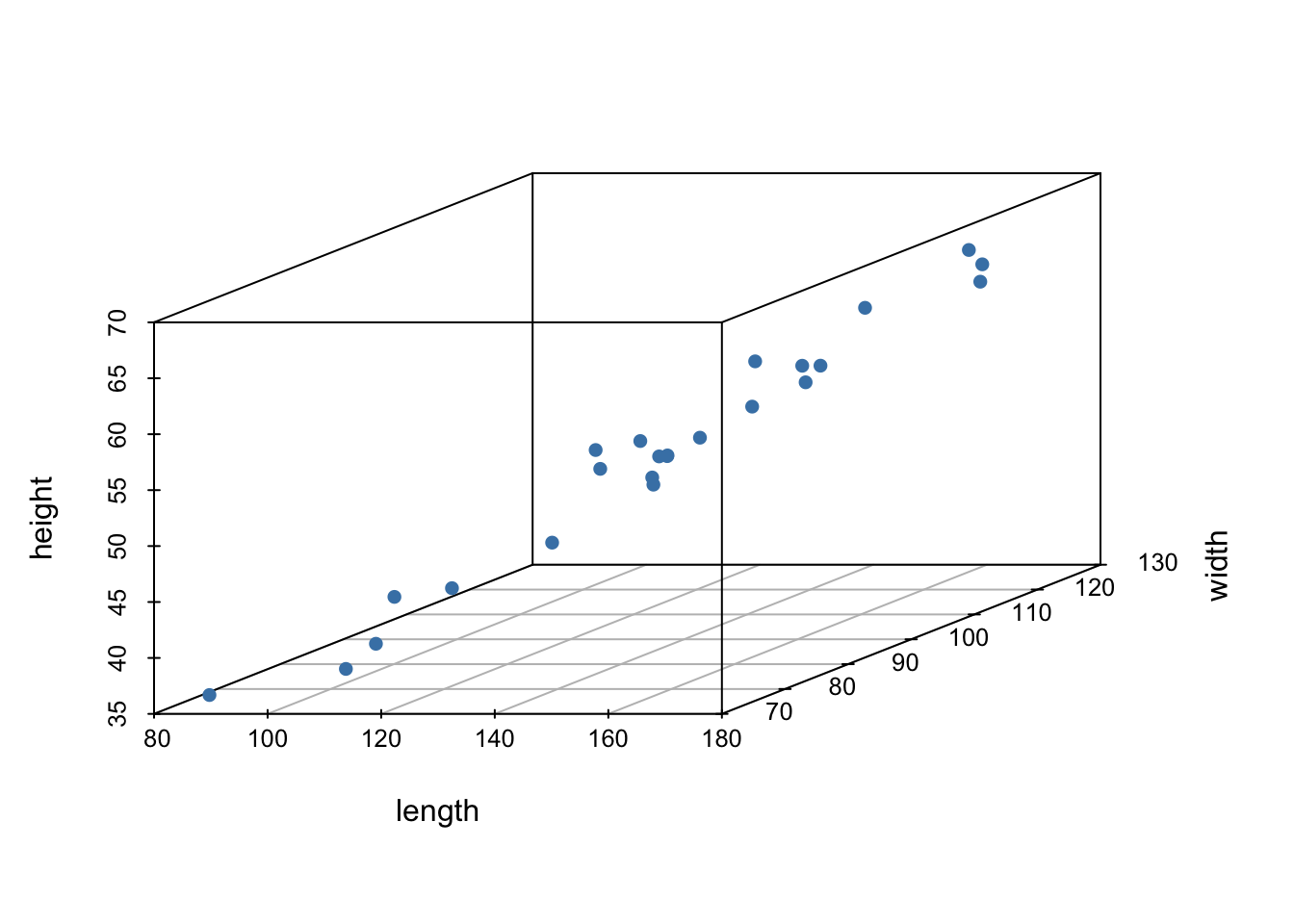
2. Perform PCA on the raw data
Again, you can choose to use the existing function or do it manually.
If we choose to use the principal function, this is what we
need to do:
(turtle.pca <- principal(turtle, nfactors = 3, rotate = 'none')) # no rotation yet## Principal Components Analysis
## Call: principal(r = turtle, nfactors = 3, rotate = "none")
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 PC3 h2 u2 com
## length 0.99 -0.03 -0.12 1 7.8e-16 1
## width 0.99 -0.11 0.08 1 2.2e-16 1
## height 0.99 0.14 0.04 1 -2.2e-16 1
##
## PC1 PC2 PC3
## SS loadings 2.94 0.04 0.02
## Proportion Var 0.98 0.01 0.01
## Cumulative Var 0.98 0.99 1.00
## Proportion Explained 0.98 0.01 0.01
## Cumulative Proportion 0.98 0.99 1.00
##
## Mean item complexity = 1
## Test of the hypothesis that 3 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0
## with the empirical chi square 0 with prob < NA
##
## Fit based upon off diagonal values = 1Let’s extract the information we need from the results object:
- Check the eigenvalues and the percentage of variance explained;
- Obtain the component score coefficients;
- Obtain the component scores for each individual;
- Scree plot;
- Biplot of both the individuals and variables.
Note that on a biplot, the coordinates of individuals and variable are NOT constructed on the same space. Therefore, only the direction of the variables is informaive. The absolute position of the variables are not.
# eigen values (also shown as SS loadings)
turtle.pca$values## [1] 2.94130818 0.03503198 0.02365984turtle.pca$Vaccounted## PC1 PC2 PC3
## SS loadings 2.9413082 0.03503198 0.023659836
## Proportion Var 0.9804361 0.01167733 0.007886612
## Cumulative Var 0.9804361 0.99211339 1.000000000
## Proportion Explained 0.9804361 0.01167733 0.007886612
## Cumulative Proportion 0.9804361 0.99211339 1.000000000# PC score coeffcients (building PCs)
turtle.pca$weights## PC1 PC2 PC3
## length 0.3372483 -0.8502526 -5.201538
## width 0.3365585 -3.2763648 3.505714
## height 0.3361201 4.1337453 1.708711# PC scores
turtle.pca$scores## PC1 PC2 PC3
## [1,] -0.0202308468 0.8783807 0.8046362
## [2,] -0.1210346335 -0.7979641 -0.4773713
## [3,] 0.7451789719 -0.8893505 0.5331761
## [4,] -1.2578745936 1.5055037 -0.7645711
## [5,] 0.1547306823 -0.3741132 -0.1685785
## [6,] 0.4097389501 -0.6891156 0.2658934
## [7,] -2.1252862594 0.7977790 1.5708875
## [8,] 0.6451096504 -0.8129062 -0.2614634
## [9,] -0.6300649722 -0.3062626 -1.6321535
## [10,] 1.0829634266 1.6987202 -0.7345361
## [11,] 1.5590280659 -0.1698589 -0.2923177
## [12,] -0.1740049672 1.8492688 0.9056181
## [13,] 1.4872592336 -1.6535859 0.5690384
## [14,] 0.5807207677 0.1707037 2.7868447
## [15,] -0.0239821941 0.2156062 -0.5454741
## [16,] -0.2315825278 0.6562107 0.8330310
## [17,] 1.5763363041 1.1269135 -0.3030369
## [18,] -1.0718293010 -0.3476536 -0.2206636
## [19,] -0.1434733468 -0.9451201 -0.9460716
## [20,] 0.0001676537 -0.6232999 0.3849697
## [21,] 0.7002138460 1.0758744 -1.5302217
## [22,] -1.4807756507 -0.1840588 -1.3150983
## [23,] -1.6587054296 -1.6865062 0.3922987
## [24,] -0.0026028296 -0.4951652 0.1451640# They can be computed manually
scale(turtle,center=T,scale=T)%*%turtle.pca$weights## PC1 PC2 PC3
## [1,] -0.0202308468 0.8783807 0.8046362
## [2,] -0.1210346335 -0.7979641 -0.4773713
## [3,] 0.7451789719 -0.8893505 0.5331761
## [4,] -1.2578745936 1.5055037 -0.7645711
## [5,] 0.1547306823 -0.3741132 -0.1685785
## [6,] 0.4097389501 -0.6891156 0.2658934
## [7,] -2.1252862594 0.7977790 1.5708875
## [8,] 0.6451096504 -0.8129062 -0.2614634
## [9,] -0.6300649722 -0.3062626 -1.6321535
## [10,] 1.0829634266 1.6987202 -0.7345361
## [11,] 1.5590280659 -0.1698589 -0.2923177
## [12,] -0.1740049672 1.8492688 0.9056181
## [13,] 1.4872592336 -1.6535859 0.5690384
## [14,] 0.5807207677 0.1707037 2.7868447
## [15,] -0.0239821941 0.2156062 -0.5454741
## [16,] -0.2315825278 0.6562107 0.8330310
## [17,] 1.5763363041 1.1269135 -0.3030369
## [18,] -1.0718293010 -0.3476536 -0.2206636
## [19,] -0.1434733468 -0.9451201 -0.9460716
## [20,] 0.0001676537 -0.6232999 0.3849697
## [21,] 0.7002138460 1.0758744 -1.5302217
## [22,] -1.4807756507 -0.1840588 -1.3150983
## [23,] -1.6587054296 -1.6865062 0.3922987
## [24,] -0.0026028296 -0.4951652 0.1451640# scree plot
VSS.scree(turtle)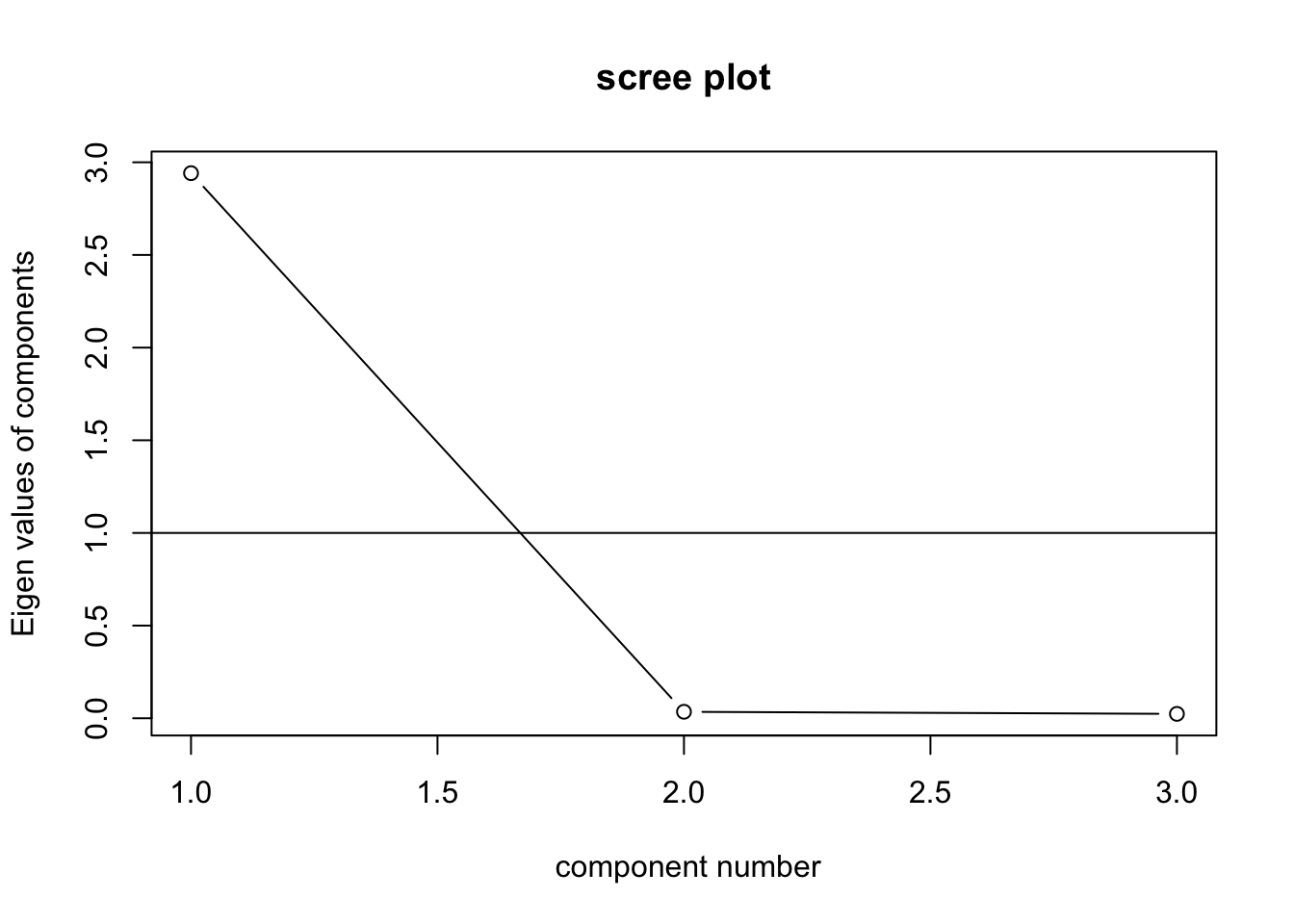
# plot of the variables and individuals
biplot(turtle.pca)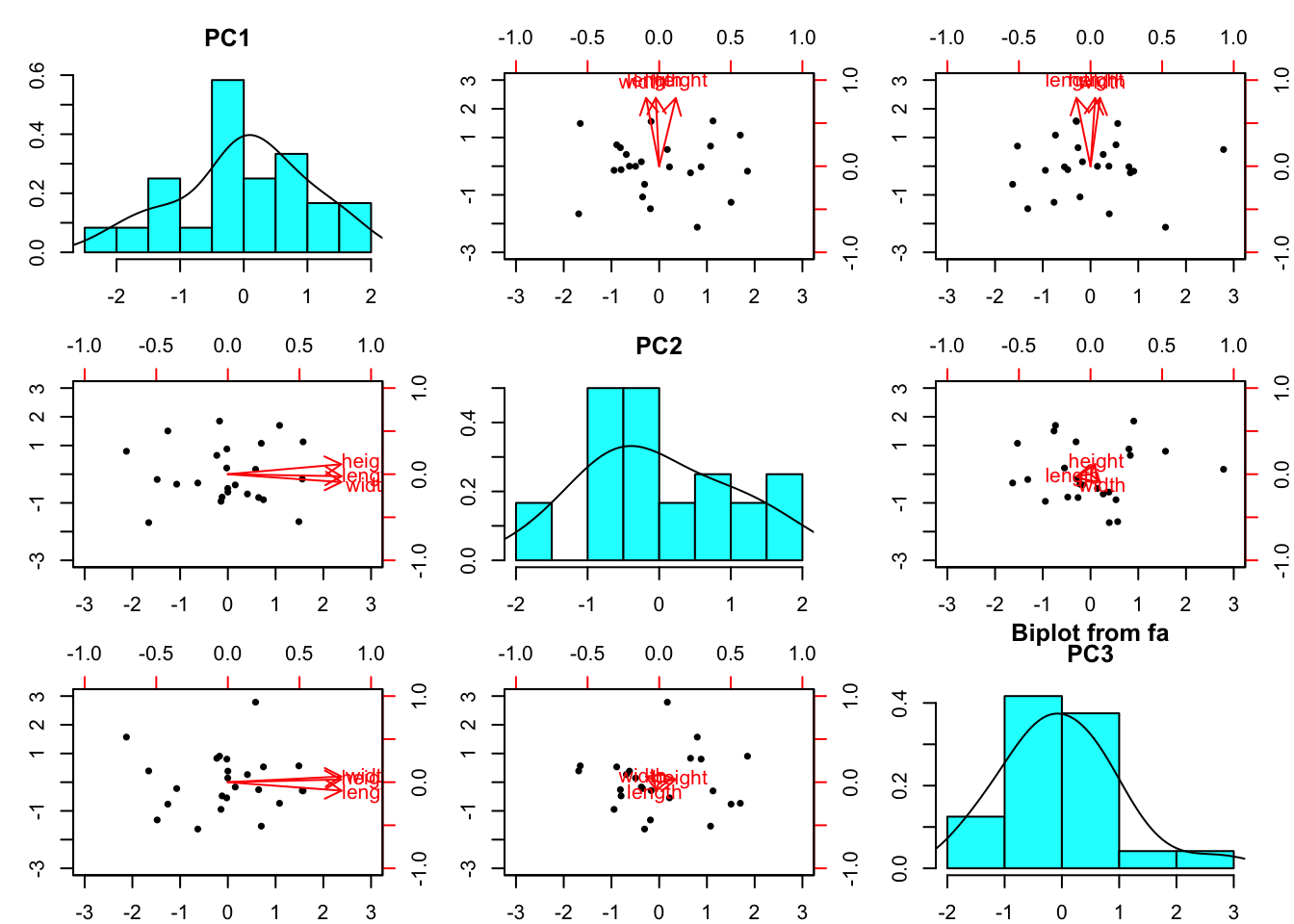
You could do more advanced plots! Here are just some examples:
- Correlation between the variables and the PCs
corrplot(turtle.pca$loadings, is.corr = T)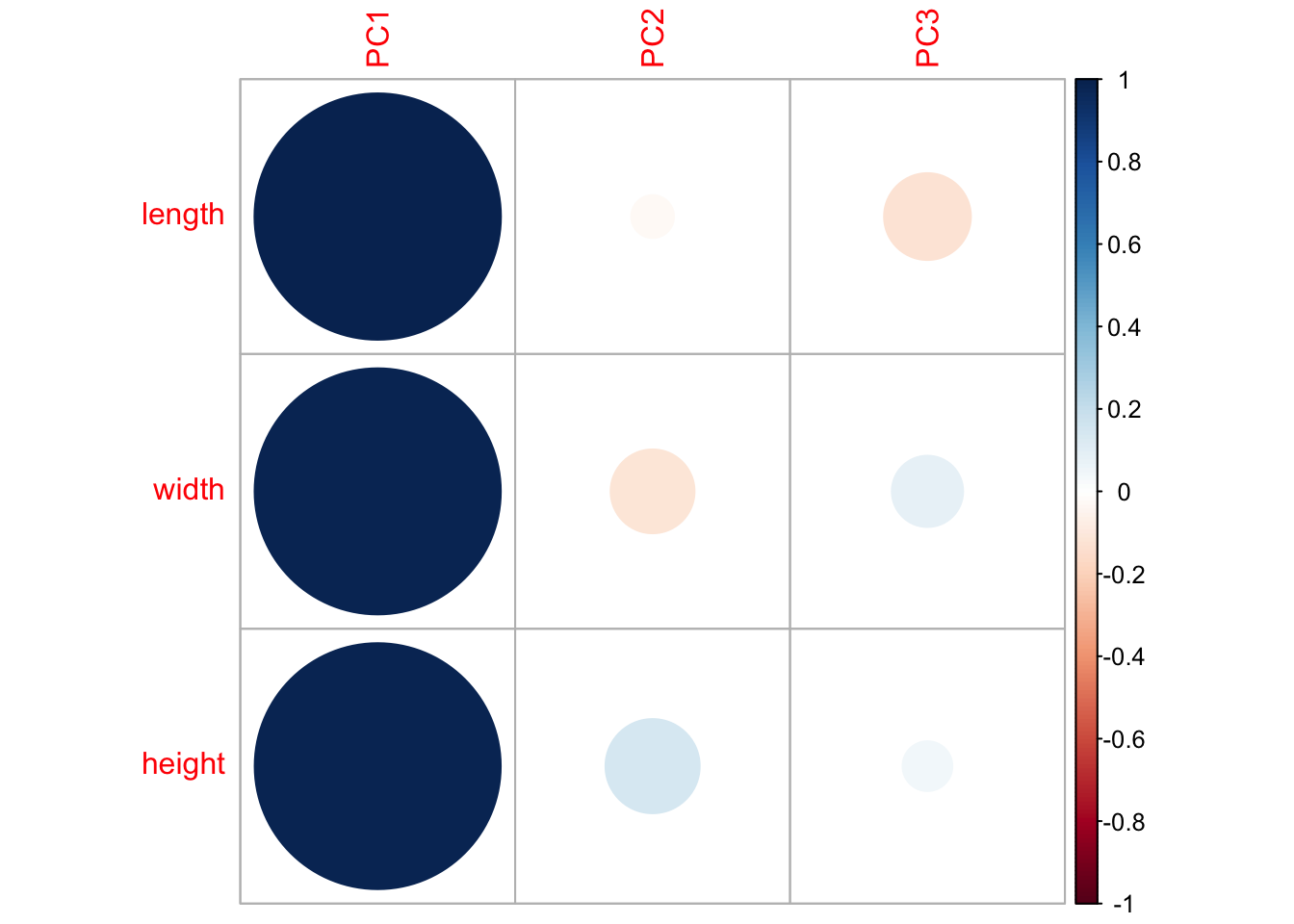
- Some advanced plots of the variables and individuals can only be
done when the built-in
prcompfunction is used for PCA.
# the variables are scaled to have unit variance
pca3 <- prcomp(turtle, scale = TRUE)
get_eigenvalue(pca3)## eigenvalue variance.percent cumulative.variance.percent
## Dim.1 2.94130818 98.0436061 98.04361
## Dim.2 0.03503198 1.1677327 99.21134
## Dim.3 0.02365984 0.7886612 100.00000fviz_eig(pca3) # scree plot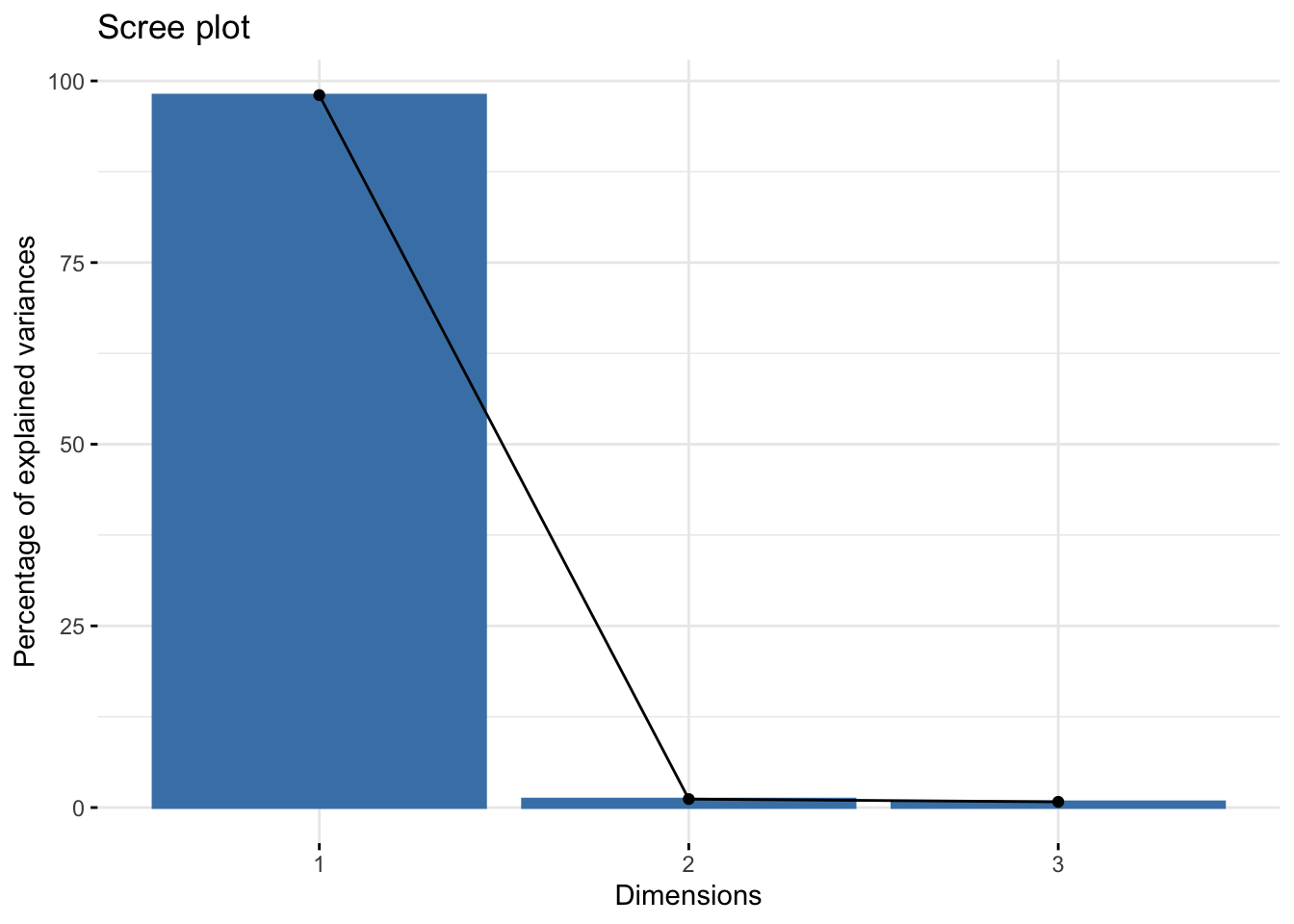
# Variable plot in person space
fviz_pca_var(pca3)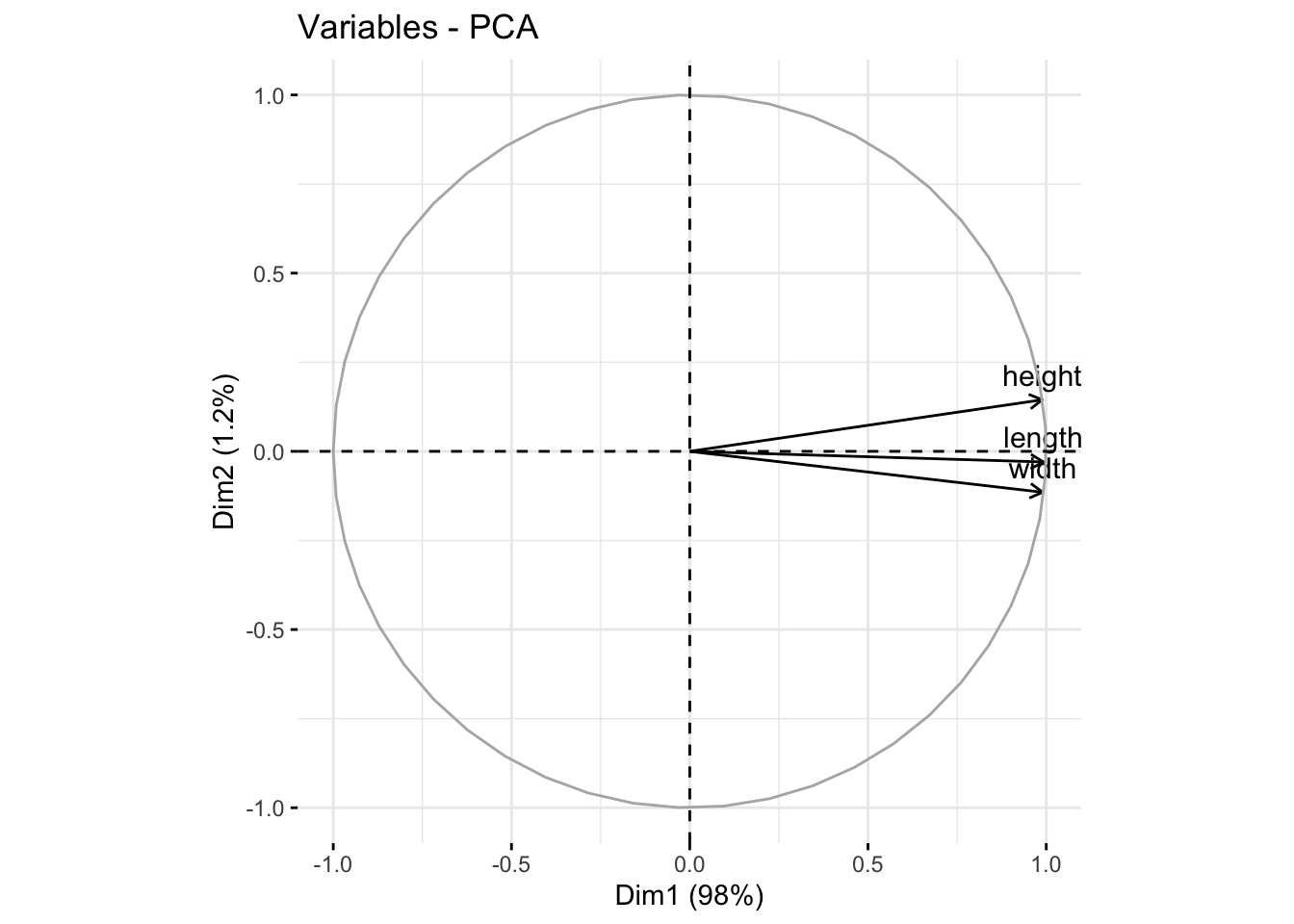
# individuals in variable space
fviz_pca_ind(pca3,col.ind = "darkred")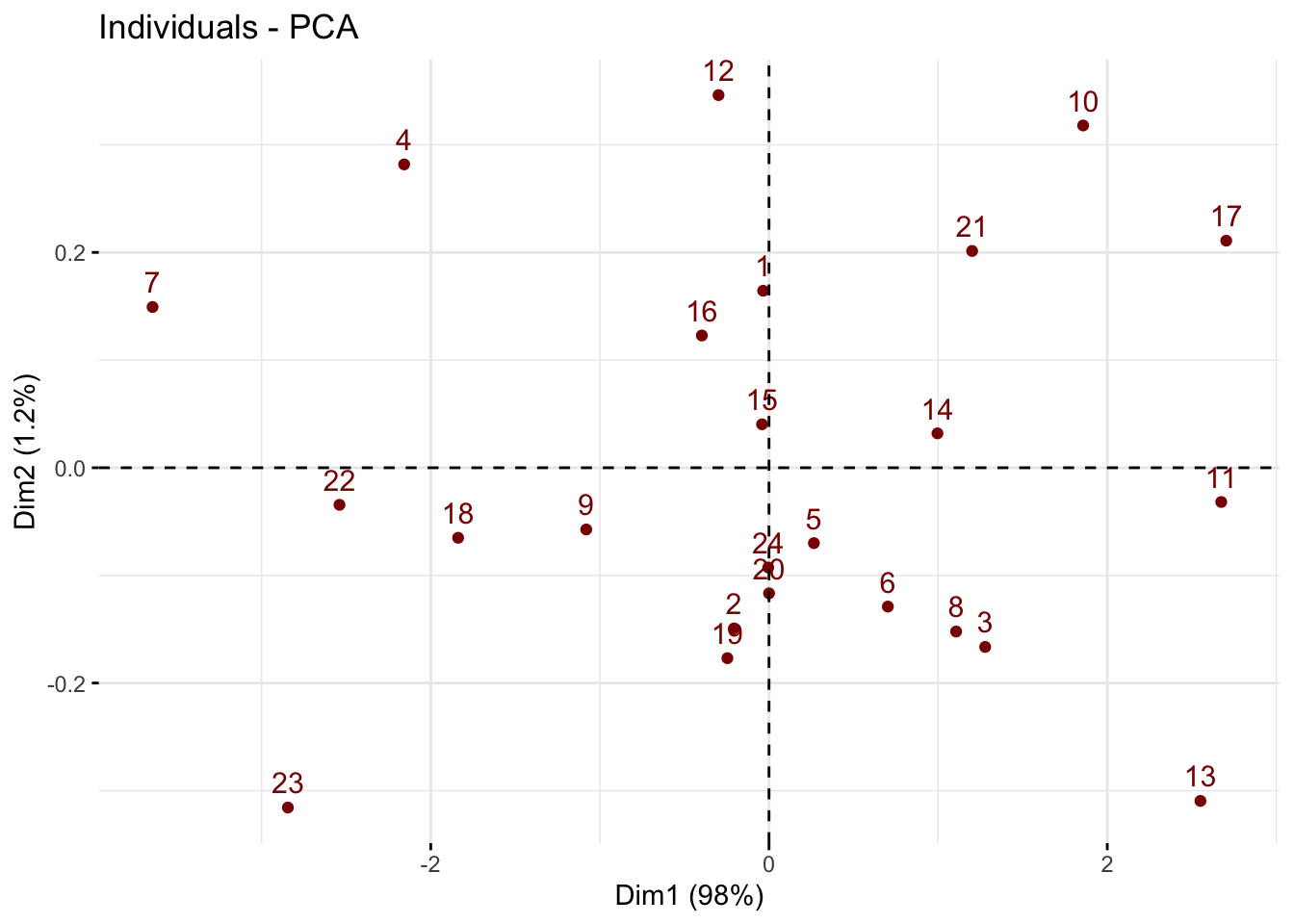
# Plot both variables and individuals
fviz_pca_biplot(pca3, repel = TRUE,
col.var = "#2E9FDF", # Variables color
col.ind = "darkred" # Individuals color
)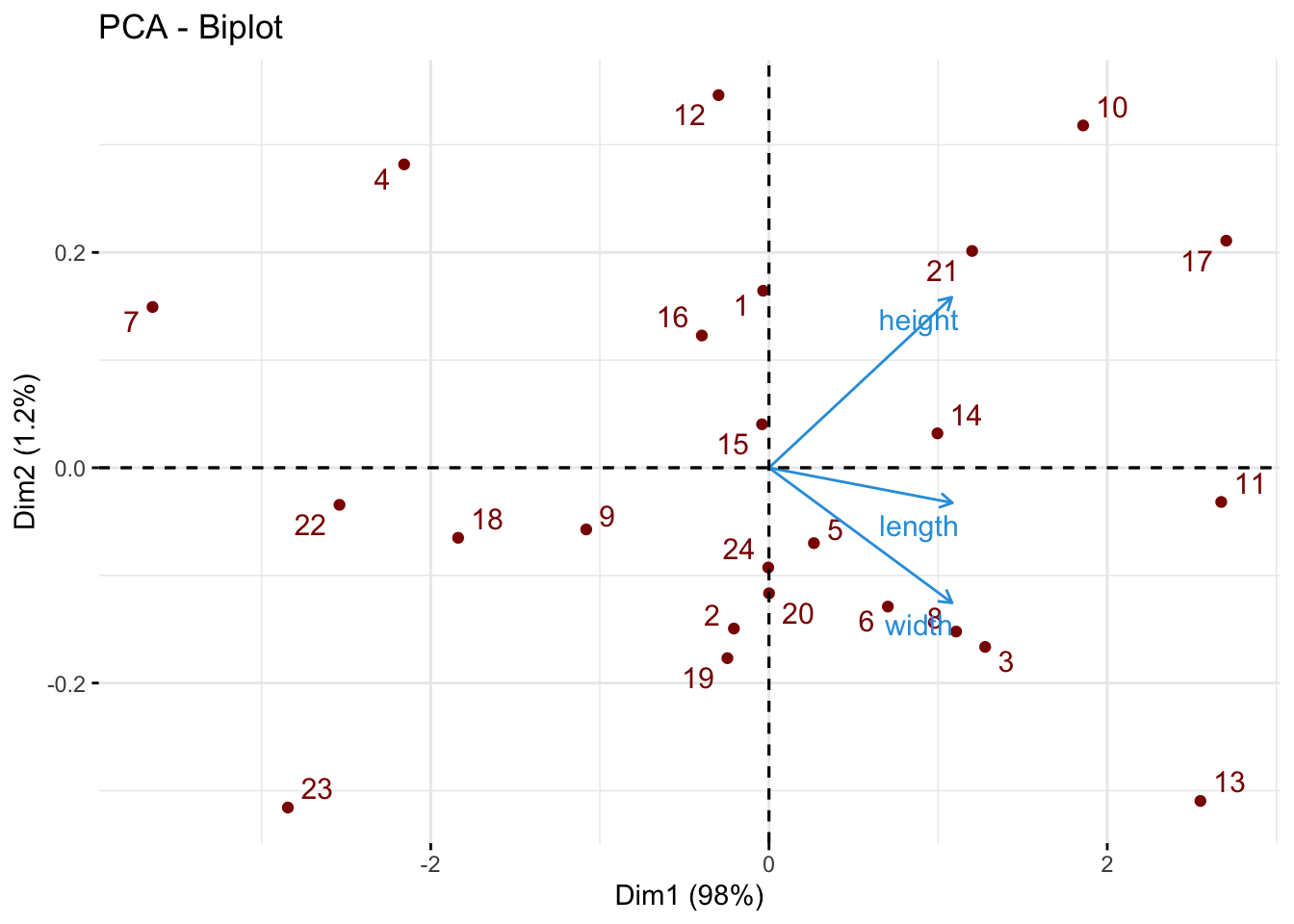
3. Decide how many components to keep and interpret the components
In this example, we decided to retain only one principal component.
(turtle.pca1 <- principal(turtle, nfactors = 1, rotate = F)) # standarize the variables## Principal Components Analysis
## Call: principal(r = turtle, nfactors = 1, rotate = F)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 h2 u2 com
## length 0.99 0.98 0.016 1
## width 0.99 0.98 0.020 1
## height 0.99 0.98 0.023 1
##
## PC1
## SS loadings 2.94
## Proportion Var 0.98
##
## Mean item complexity = 1
## Test of the hypothesis that 1 component is sufficient.
##
## The root mean square of the residuals (RMSR) is 0.01
## with the empirical chi square 0.01 with prob < NA
##
## Fit based upon off diagonal values = 1turtle.pca1$communality #communality## length width height
## 0.9839672 0.9799463 0.9773947turtle.pca1$loadings #loadings (component matrix)##
## Loadings:
## PC1
## length 0.992
## width 0.990
## height 0.989
##
## PC1
## SS loadings 2.941
## Proportion Var 0.980turtle.pca1$weights #component score coefficients## PC1
## length 0.3372483
## width 0.3365585
## height 0.3361201turtle.pca1$Vaccounted #var explained## PC1
## SS loadings 2.9413082
## Proportion Var 0.9804361Example 3-1: PCA with medical school data (no rotation)
1. Read data and explore the data
describe(med.data)## vars n mean sd median trimmed mad min max range skew kurtosis
## medicine 1 61 81.84 4.76 83 81.78 4.45 70 94 24 0.08 0.09
## psychiat 2 61 78.49 5.54 79 78.84 5.93 54 88 34 -1.29 4.35
## obgyn 3 61 78.82 4.71 79 78.88 5.93 69 90 21 -0.06 -0.40
## pediatri 4 61 79.85 5.61 80 79.88 4.45 65 95 30 -0.05 0.25
## pubhlth 5 61 79.62 3.84 80 79.84 4.45 70 87 17 -0.41 -0.38
## surgery 6 61 80.18 5.23 81 80.53 4.45 64 90 26 -0.68 0.64
## se
## medicine 0.61
## psychiat 0.71
## obgyn 0.60
## pediatri 0.72
## pubhlth 0.49
## surgery 0.67(med.cor <- cor(med.data))## medicine psychiat obgyn pediatri pubhlth surgery
## medicine 1.00000000 0.03470021 0.4813512 0.6327648 0.1969204 0.5249143
## psychiat 0.03470021 1.00000000 0.2223908 0.3417282 0.8425290 0.3900493
## obgyn 0.48135119 0.22239077 1.0000000 0.5357973 0.3660219 0.4661219
## pediatri 0.63276481 0.34172819 0.5357973 1.0000000 0.4524968 0.5384566
## pubhlth 0.19692041 0.84252903 0.3660219 0.4524968 1.0000000 0.4639141
## surgery 0.52491429 0.39004934 0.4661219 0.5384566 0.4639141 1.00000002. Perform PCA on the raw data
(med.pca <- principal(med.data, nfactors = 6, rotate = F))## Specified rotation not found, rotate='none' used## Principal Components Analysis
## Call: principal(r = med.data, nfactors = 6, rotate = F)
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 PC3 PC4 PC5 PC6 h2 u2 com
## medicine 0.66 -0.60 -0.23 0.15 0.36 0.05 1 3.3e-16 3.0
## psychiat 0.64 0.72 -0.03 0.06 0.05 0.26 1 -1.1e-15 2.3
## obgyn 0.70 -0.29 0.63 -0.15 0.02 0.03 1 -2.2e-16 2.5
## pediatri 0.81 -0.25 -0.07 0.38 -0.35 -0.01 1 -1.1e-15 2.1
## pubhlth 0.76 0.57 0.03 0.08 0.14 -0.26 1 1.0e-15 2.3
## surgery 0.78 -0.11 -0.31 -0.51 -0.13 -0.02 1 -1.1e-15 2.2
##
## PC1 PC2 PC3 PC4 PC5 PC6
## SS loadings 3.19 1.37 0.55 0.46 0.30 0.14
## Proportion Var 0.53 0.23 0.09 0.08 0.05 0.02
## Cumulative Var 0.53 0.76 0.85 0.93 0.98 1.00
## Proportion Explained 0.53 0.23 0.09 0.08 0.05 0.02
## Cumulative Proportion 0.53 0.76 0.85 0.93 0.98 1.00
##
## Mean item complexity = 2.4
## Test of the hypothesis that 6 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0
## with the empirical chi square 0 with prob < NA
##
## Fit based upon off diagonal values = 1med.pca$weights## PC1 PC2 PC3 PC4 PC5 PC6
## medicine 0.2061306 -0.43904427 -0.41375157 0.3306493 1.21981449 0.35113329
## psychiat 0.2012506 0.52444502 -0.05475583 0.1200840 0.17403833 1.86083343
## obgyn 0.2206947 -0.21367803 1.14852079 -0.3330822 0.07189835 0.23946503
## pediatri 0.2550863 -0.18467144 -0.12429064 0.8254373 -1.19382288 -0.07494406
## pubhlth 0.2380869 0.41851497 0.05437260 0.1722619 0.48083498 -1.89754838
## surgery 0.2458487 -0.08306974 -0.56297440 -1.0998042 -0.45673081 -0.11723917VSS.scree(med.data)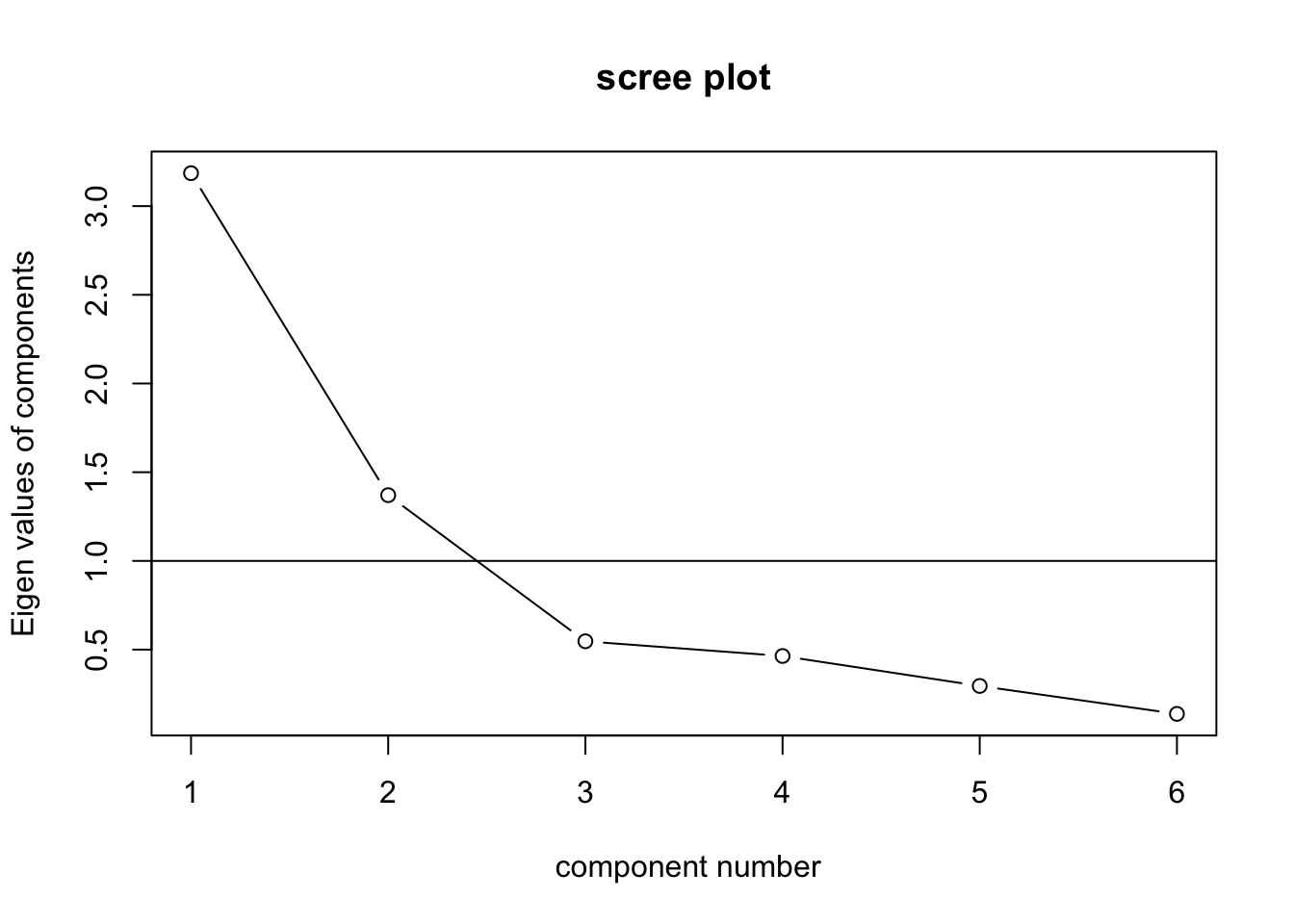
3. Decide how many components to keep and interpret the components
You could run different tests to see how many components to keep:
#MAP
VSS(med.data)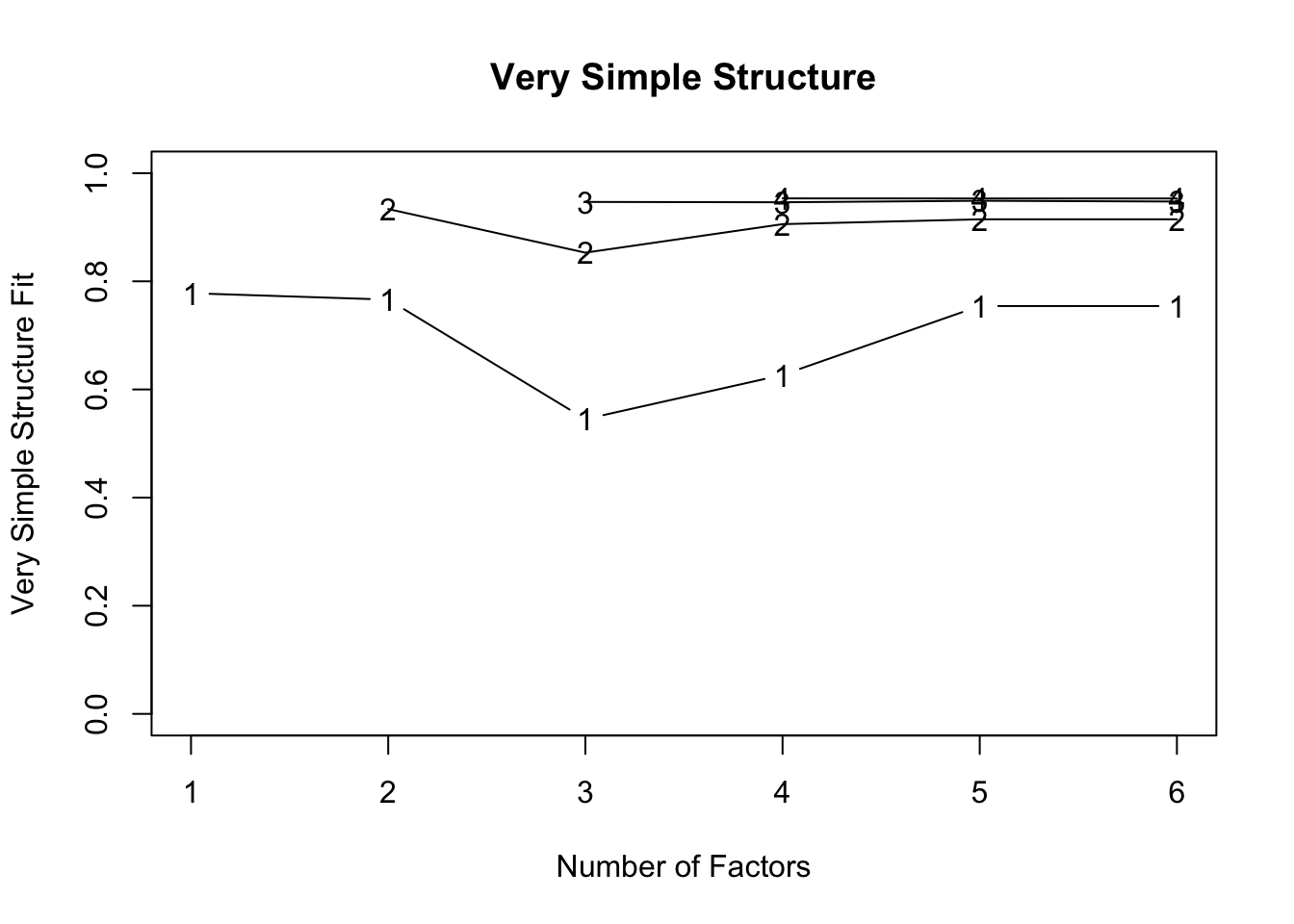
##
## Very Simple Structure
## Call: vss(x = x, n = n, rotate = rotate, diagonal = diagonal, fm = fm,
## n.obs = n.obs, plot = plot, title = title, use = use, cor = cor)
## VSS complexity 1 achieves a maximimum of 0.78 with 1 factors
## VSS complexity 2 achieves a maximimum of 0.93 with 2 factors
##
## The Velicer MAP achieves a minimum of 0.11 with 2 factors
## BIC achieves a minimum of -14.7 with 2 factors
## Sample Size adjusted BIC achieves a minimum of -2.12 with 2 factors
##
## Statistics by number of factors
## vss1 vss2 map dof chisq prob sqresid fit RMSEA BIC SABIC complex
## 1 0.78 0.00 0.15 9 7.4e+01 2.0e-12 2.81 0.78 0.34 37 65.8 1.0
## 2 0.77 0.93 0.11 4 1.7e+00 7.8e-01 0.84 0.93 0.00 -15 -2.1 1.2
## 3 0.55 0.85 0.23 0 2.5e-04 NA 0.67 0.95 NA NA NA 1.7
## 4 0.63 0.91 0.44 -3 2.7e-05 NA 0.59 0.95 NA NA NA 1.6
## 5 0.75 0.91 1.00 -5 4.8e-12 NA 0.58 0.95 NA NA NA 1.5
## 6 0.75 0.91 NA -6 0.0e+00 NA 0.58 0.95 NA NA NA 1.5
## eChisq SRMR eCRMS eBIC
## 1 5.3e+01 1.7e-01 0.219 16
## 2 4.1e-01 1.5e-02 0.029 -16
## 3 3.6e-05 1.4e-04 NA NA
## 4 2.5e-06 3.7e-05 NA NA
## 5 6.8e-13 1.9e-08 NA NA
## 6 3.4e-28 4.3e-16 NA NA# Cattell-Nelson-Gorsuch scree plot
(CNG <- nCng(med.pca$values, details = T))## [1] 3# Parallel Analysis
pscree <- fa.parallel(med.data, nfactors = 6, n.iter = 100, fa = 'pc', sim = T)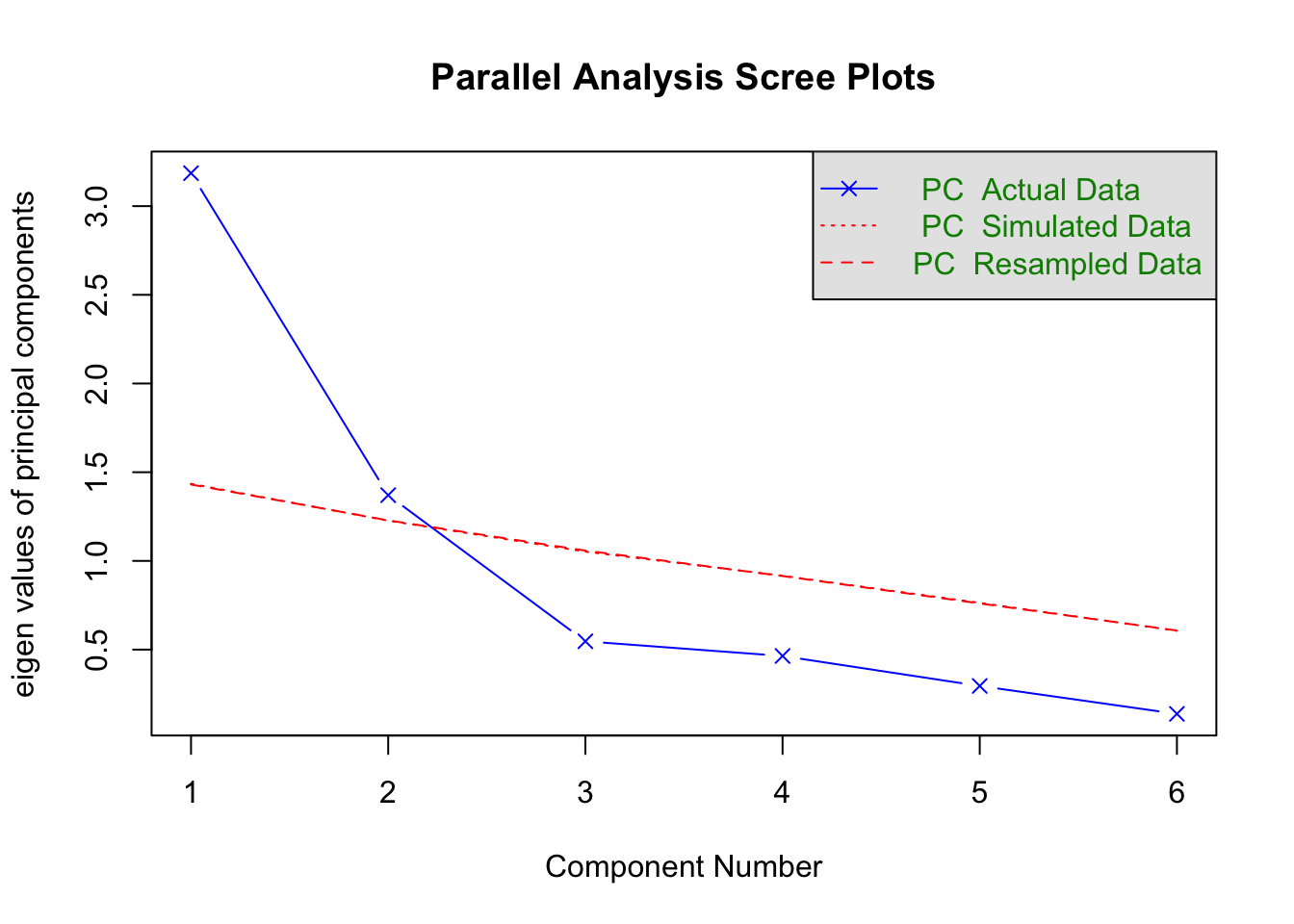
## Parallel analysis suggests that the number of factors = NA and the number of components = 2plot(pscree, fa = "pc") 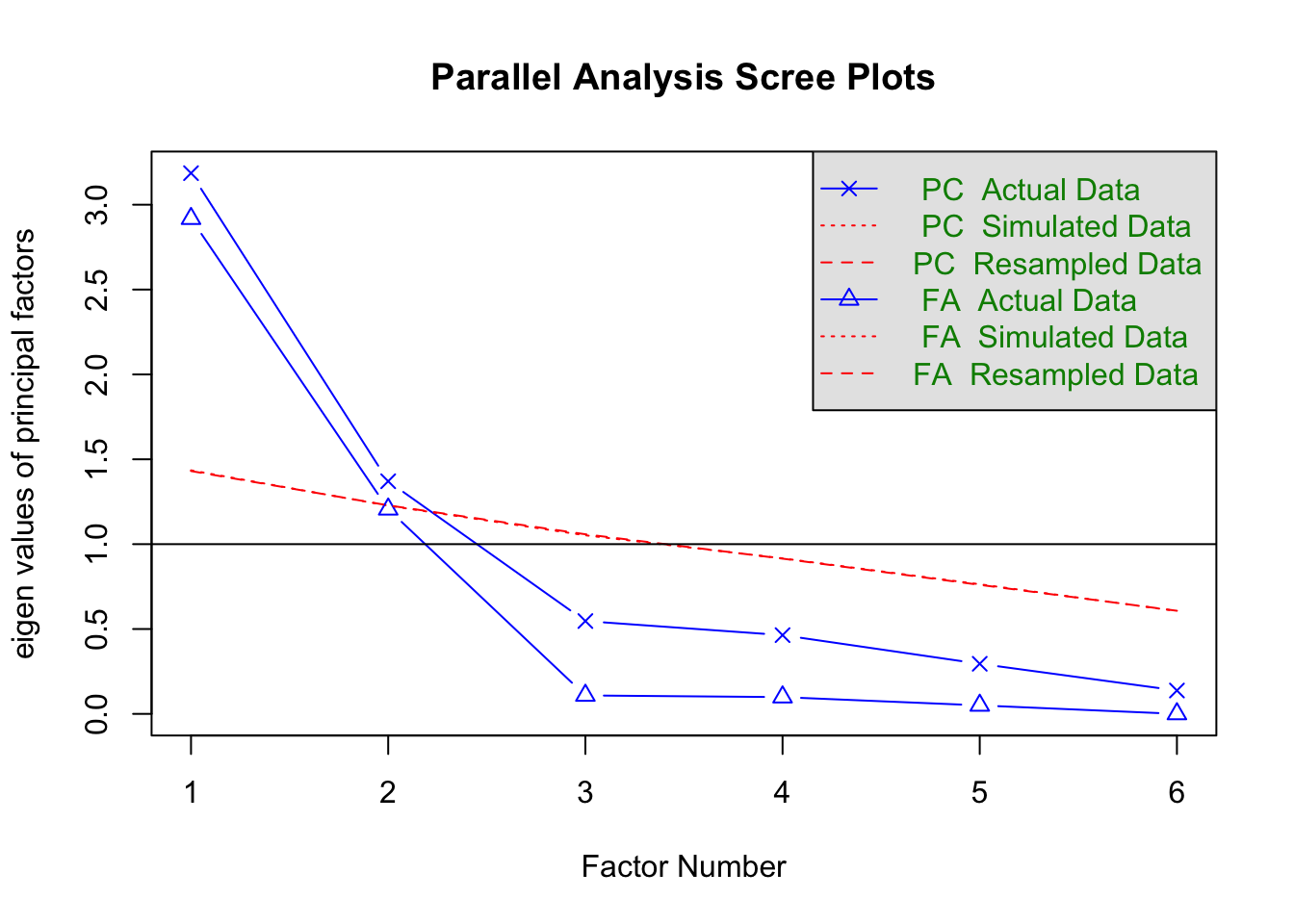
For this example we choose to retain the first two principal components.
(med.pca2 <- principal(med.data, nfactors = 2, rotate = 'none')) # standarize the variables## Principal Components Analysis
## Call: principal(r = med.data, nfactors = 2, rotate = "none")
## Standardized loadings (pattern matrix) based upon correlation matrix
## PC1 PC2 h2 u2 com
## medicine 0.66 -0.60 0.79 0.207 2.0
## psychiat 0.64 0.72 0.93 0.072 2.0
## obgyn 0.70 -0.29 0.58 0.420 1.3
## pediatri 0.81 -0.25 0.72 0.276 1.2
## pubhlth 0.76 0.57 0.90 0.096 1.9
## surgery 0.78 -0.11 0.63 0.374 1.0
##
## PC1 PC2
## SS loadings 3.19 1.37
## Proportion Var 0.53 0.23
## Cumulative Var 0.53 0.76
## Proportion Explained 0.70 0.30
## Cumulative Proportion 0.70 1.00
##
## Mean item complexity = 1.6
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.08
## with the empirical chi square 10.46 with prob < 0.033
##
## Fit based upon off diagonal values = 0.97med.pca2$communality #communality## medicine psychiat obgyn pediatri pubhlth surgery
## 0.7933364 0.9277259 0.5801000 0.7244654 0.9043401 0.6264004med.pca2$loadings #loadings (component matrix)##
## Loadings:
## PC1 PC2
## medicine 0.657 -0.602
## psychiat 0.641 0.719
## obgyn 0.703 -0.293
## pediatri 0.813 -0.253
## pubhlth 0.758 0.574
## surgery 0.783 -0.114
##
## PC1 PC2
## SS loadings 3.186 1.371
## Proportion Var 0.531 0.228
## Cumulative Var 0.531 0.759med.pca2$weights #component score coefficients## PC1 PC2
## medicine 0.2061306 -0.43904427
## psychiat 0.2012506 0.52444502
## obgyn 0.2206947 -0.21367803
## pediatri 0.2550863 -0.18467144
## pubhlth 0.2380869 0.41851497
## surgery 0.2458487 -0.08306974med.pca2$Vaccounted #var explained, correct percentage## PC1 PC2
## SS loadings 3.1857910 1.3705771
## Proportion Var 0.5309652 0.2284295
## Cumulative Var 0.5309652 0.7593947
## Proportion Explained 0.6991953 0.3008047
## Cumulative Proportion 0.6991953 1.0000000Note that now the “Proportion Var” is different from the “Proportion Explained”. “Proportion Var” is calculated out of the total variance in all the variables:
\[ \begin{aligned} 3.186/6=0.531. \end{aligned} \] “Proportion Explained” is calculated out of the extracted sum of squared loadings:
\[ \begin{aligned} 3.186/(3.186+1.371)=0.699. \end{aligned} \]
med.pca2$scores #PC scores## PC1 PC2
## [1,] 0.94140437 -0.15841813
## [2,] 1.06682064 0.12250987
## [3,] 2.72901614 -0.21375808
## [4,] 0.16735630 -0.15719056
## [5,] -0.48521317 -0.39298806
## [6,] 0.02110857 -1.63814304
## [7,] 0.71069897 -1.87333787
## [8,] -0.36955096 0.59458739
## [9,] -1.42615444 -0.02555542
## [10,] -0.42501442 -1.01845328
## [11,] -0.49079206 -0.08410739
## [12,] -0.66387770 -0.33730177
## [13,] -0.32148168 0.40597274
## [14,] 0.05056575 0.08960764
## [15,] 1.08793470 0.46636836
## [16,] 0.74578638 0.47214470
## [17,] -0.12944477 0.45870431
## [18,] 0.83226281 0.86617936
## [19,] -0.92478559 0.12336735
## [20,] 1.02077013 0.01297160
## [21,] 0.96763210 -0.59813729
## [22,] 0.09113695 -1.17759657
## [23,] 1.12199366 -0.48522858
## [24,] 0.06110789 -0.78056387
## [25,] 0.37900831 0.48702510
## [26,] -0.21917042 1.57630710
## [27,] 0.37161113 0.42400487
## [28,] 0.99561518 1.40121364
## [29,] 0.99000650 -0.37410721
## [30,] -0.62966716 0.93596412
## [31,] -0.78801754 0.48089988
## [32,] -0.33135180 -0.26834151
## [33,] -0.42278792 -0.34122155
## [34,] -1.87756846 1.81811122
## [35,] 1.96683959 -1.97148651
## [36,] -0.37640504 2.32782506
## [37,] 1.42267625 -0.12574966
## [38,] 0.47785680 2.13173533
## [39,] 0.63043156 0.07650810
## [40,] 0.24932217 1.06401538
## [41,] -2.54606268 -0.21884033
## [42,] 0.39849388 -0.11455697
## [43,] -1.14849808 -0.57793067
## [44,] -0.49023131 -0.14197975
## [45,] -1.25731991 0.47756996
## [46,] 1.21917963 0.30376382
## [47,] 0.18175292 0.08978713
## [48,] 0.06894520 0.48862733
## [49,] -1.02976747 -0.28753113
## [50,] 0.50756884 0.06005134
## [51,] 0.08329042 -0.34956918
## [52,] 1.24021716 -0.26546890
## [53,] 0.86502211 1.10253522
## [54,] -1.10507899 -1.01217769
## [55,] -1.24538946 2.04522645
## [56,] -1.60988005 -0.37774949
## [57,] 0.28226965 -0.33394776
## [58,] 0.28226965 -0.33394776
## [59,] -1.44156799 0.29435049
## [60,] -0.67237455 -1.63822388
## [61,] -1.80051872 -3.52432503We can get the biplot with only the first two principal components.
biplot(med.pca2, main = "Biplot with 2 principal components")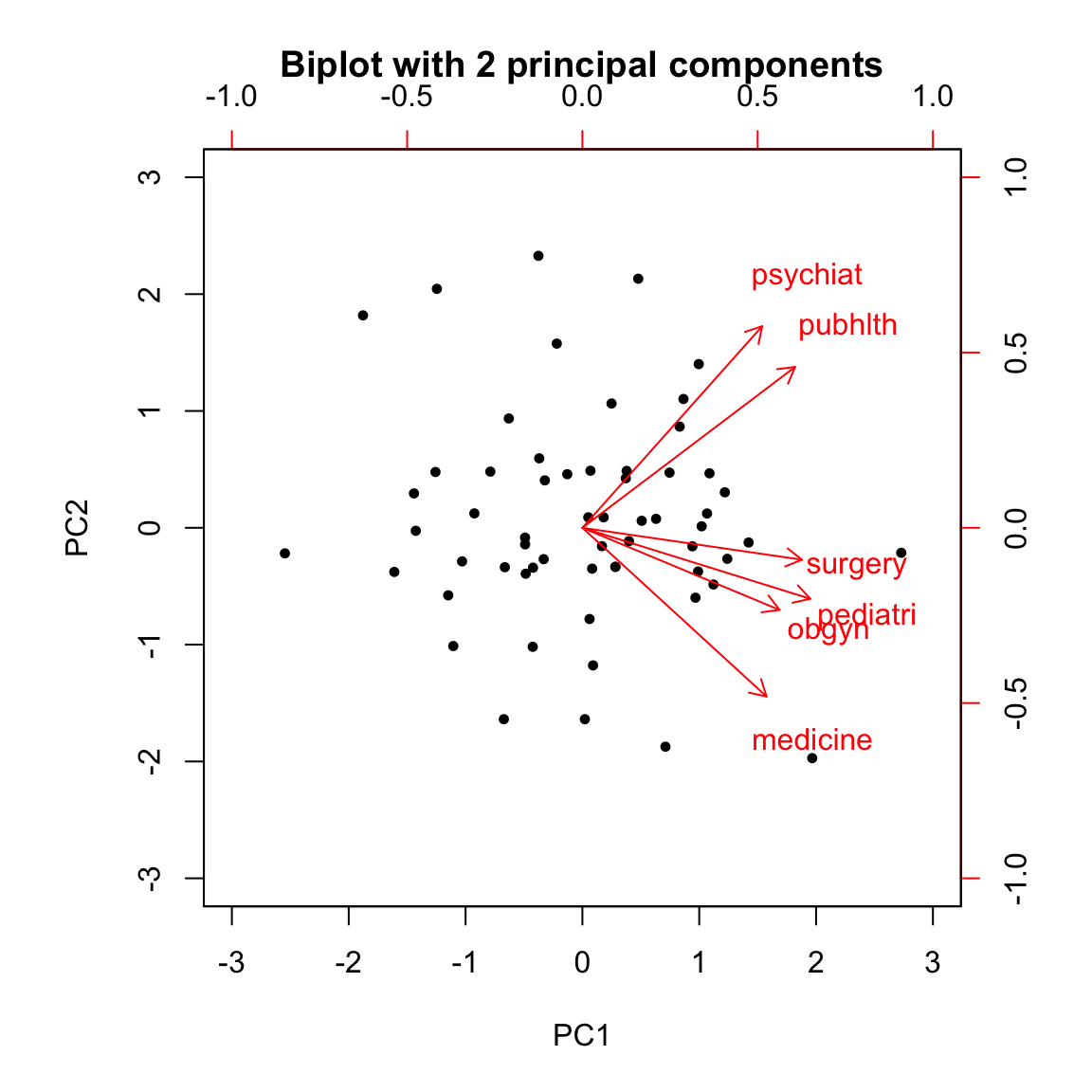
4. Some further follow-up procedures
The reproduced correlation matrix can be obtained using the
factor.model() function and the residual matrix can be
obtained using the factor.residuals() function.
# reproduced correlations
factor.model(med.pca2$loadings)## medicine psychiat obgyn pediatri pubhlth surgery
## medicine 0.7933364 -0.0114979 0.6379378 0.6859646 0.1529309 0.5828444
## psychiat -0.0114979 0.9277259 0.2402719 0.3390943 0.8986077 0.4203202
## obgyn 0.6379378 0.2402719 0.5801000 0.6454903 0.3653005 0.5840173
## pediatri 0.6859646 0.3390943 0.6454903 0.7244654 0.4712087 0.6653042
## pubhlth 0.1529309 0.8986077 0.3653005 0.4712087 0.9043401 0.5287635
## surgery 0.5828444 0.4203202 0.5840173 0.6653042 0.5287635 0.6264004# residuals
factor.residuals(med.cor, med.pca2$loadings)## medicine psychiat obgyn pediatri pubhlth
## medicine 0.20666364 0.046198110 -0.1565865912 -0.053199841 0.0439895296
## psychiat 0.04619811 0.072274127 -0.0178810971 0.002633882 -0.0560787028
## obgyn -0.15658659 -0.017881097 0.4199000063 -0.109692940 0.0007213988
## pediatri -0.05319984 0.002633882 -0.1096929398 0.275534574 -0.0187119126
## pubhlth 0.04398953 -0.056078703 0.0007213988 -0.018711913 0.0956599298
## surgery -0.05793012 -0.030270851 -0.1178954174 -0.126847618 -0.0648494424
## surgery
## medicine -0.05793012
## psychiat -0.03027085
## obgyn -0.11789542
## pediatri -0.12684762
## pubhlth -0.06484944
## surgery 0.37359957You could manually create the component loading plot using the results.
# component loading plot
plot(x = med.pca2$loadings[,1], y = med.pca2$loadings[,2], xlim = c(-1,1), ylim = c(-1,1), xlab = "PC1", ylab = "PC2", main = "Component plot")
text(PC2~PC1, labels = rownames(med.pca2$loadings), data = as.data.frame(med.pca2$loadings[,1:2]), cex = 0.5, font = 2, pos = 4)
abline(v = 0, col = "red", lty = 2)
abline(h = 0, col = "red", lty = 2)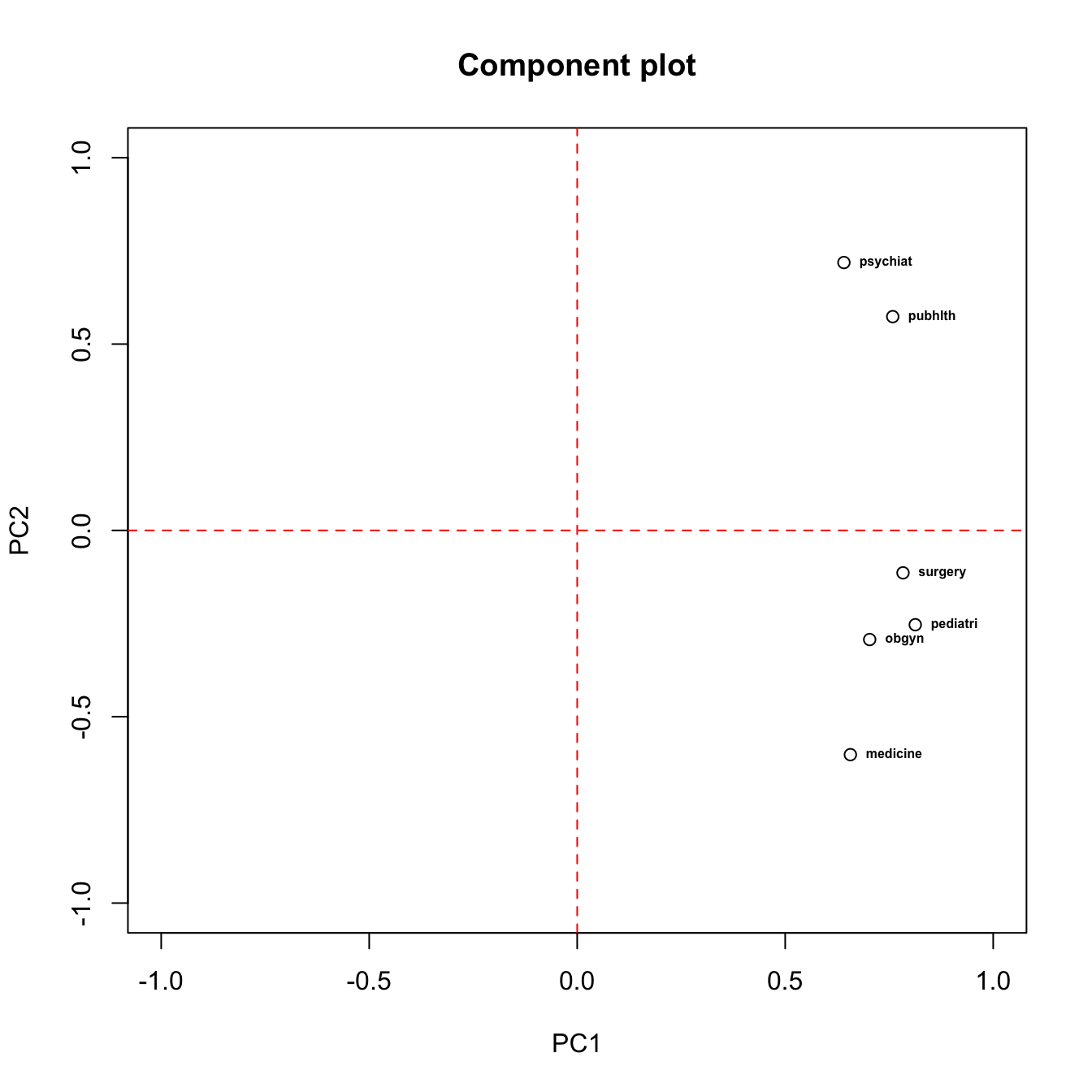
Example 3-2: PCA with medical school data (with rotation)
Varimax rotation
(med.pca.var <- principal(med.data, nfactors = 2))## Principal Components Analysis
## Call: principal(r = med.data, nfactors = 2)
## Standardized loadings (pattern matrix) based upon correlation matrix
## RC1 RC2 h2 u2 com
## medicine 0.89 -0.09 0.79 0.207 1.0
## psychiat 0.08 0.96 0.93 0.072 1.0
## obgyn 0.74 0.19 0.58 0.420 1.1
## pediatri 0.80 0.28 0.72 0.276 1.2
## pubhlth 0.26 0.91 0.90 0.096 1.2
## surgery 0.70 0.38 0.63 0.374 1.5
##
## RC1 RC2
## SS loadings 2.54 2.02
## Proportion Var 0.42 0.34
## Cumulative Var 0.42 0.76
## Proportion Explained 0.56 0.44
## Cumulative Proportion 0.56 1.00
##
## Mean item complexity = 1.2
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.08
## with the empirical chi square 10.46 with prob < 0.033
##
## Fit based upon off diagonal values = 0.97med.pca.var$communality #communality## medicine psychiat obgyn pediatri pubhlth surgery
## 0.7933364 0.9277259 0.5801000 0.7244654 0.9043401 0.6264004med.pca.var$loadings #loadings (component matrix)##
## Loadings:
## RC1 RC2
## medicine 0.886
## psychiat 0.960
## obgyn 0.739 0.186
## pediatri 0.803 0.283
## pubhlth 0.265 0.913
## surgery 0.696 0.377
##
## RC1 RC2
## SS loadings 2.536 2.020
## Proportion Var 0.423 0.337
## Cumulative Var 0.423 0.759med.pca.var$weights #component score coefficients## RC1 RC2
## medicine 0.4277975 -0.228558486
## psychiat -0.1524021 0.540664375
## obgyn 0.3046716 -0.039238451
## pediatri 0.3148835 0.004577979
## pubhlth -0.0595218 0.477804693
## surgery 0.2467098 0.080476513med.pca.var$Vaccounted #var explained## RC1 RC2
## SS loadings 2.5363879 2.0199802
## Proportion Var 0.4227313 0.3366634
## Cumulative Var 0.4227313 0.7593947
## Proportion Explained 0.5566688 0.4433312
## Cumulative Proportion 0.5566688 1.0000000med.pca.var$scores #PC scores## RC1 RC2
## [1,] 0.84919698 0.43612268
## [2,] 0.78167519 0.73627362
## [3,] 2.31489198 1.46099170
## [4,] 0.22813947 -0.02587246
## [5,] -0.15379385 -0.60516022
## [6,] 0.99673372 -1.30018464
## [7,] 1.69004882 -1.07620760
## [8,] -0.65179735 0.25546487
## [9,] -1.12763688 -0.87350136
## [10,] 0.26855704 -1.07040248
## [11,] -0.34301459 -0.36095967
## [12,] -0.33028333 -0.66739718
## [13,] -0.50045907 0.13306034
## [14,] -0.01307327 0.10205643
## [15,] 0.59292505 1.02447121
## [16,] 0.31527189 0.82445229
## [17,] -0.37810058 0.29018192
## [18,] 0.14889154 1.19195612
## [19,] -0.81491386 -0.45427228
## [20,] 0.81028802 0.62094545
## [21,] 1.13322374 0.09941860
## [22,] 0.77738937 -0.88921616
## [23,] 1.18939559 0.28223160
## [24,] 0.51584814 -0.58899477
## [25,] 0.01243504 0.61699766
## [26,] -1.11847504 1.13216312
## [27,] 0.04420102 0.56206870
## [28,] -0.04021599 1.71843881
## [29,] 1.01715622 0.29233937
## [30,] -1.06444142 0.37346220
## [31,] -0.91915753 -0.08594055
## [32,] -0.10504357 -0.41323968
## [33,] -0.13472911 -0.52633624
## [34,] -2.59214719 0.33401296
## [35,] 2.75542709 -0.40353268
## [36,] -1.69398614 1.64038448
## [37,] 1.21534907 0.75016485
## [38,] -0.89209292 1.99419478
## [39,] 0.45946723 0.43839172
## [40,] -0.43660898 1.00182977
## [41,] -1.90952409 -1.69824732
## [42,] 0.38787318 0.14654375
## [43,] -0.57473221 -1.15010199
## [44,] -0.30795020 -0.40700327
## [45,] -1.29326542 -0.36931149
## [46,] 0.79536306 0.97266080
## [47,] 0.09195297 0.18066683
## [48,] -0.23700833 0.43282464
## [49,] -0.65327709 -0.84635941
## [50,] 0.37084810 0.35171576
## [51,] 0.27583577 -0.23032702
## [52,] 1.15269592 0.52905998
## [53,] 0.03377410 1.40096626
## [54,] -0.28020130 -1.47213807
## [55,] -2.22136173 0.89414665
## [56,] -1.06421814 -1.26564143
## [57,] 0.42595442 -0.09879318
## [58,] 0.42595442 -0.09879318
## [59,] -1.33133362 -0.62634756
## [60,] 0.44102368 -1.71504027
## [61,] 0.66505496 -3.90133778Let’s see how the components look differently than they were before
rotation:
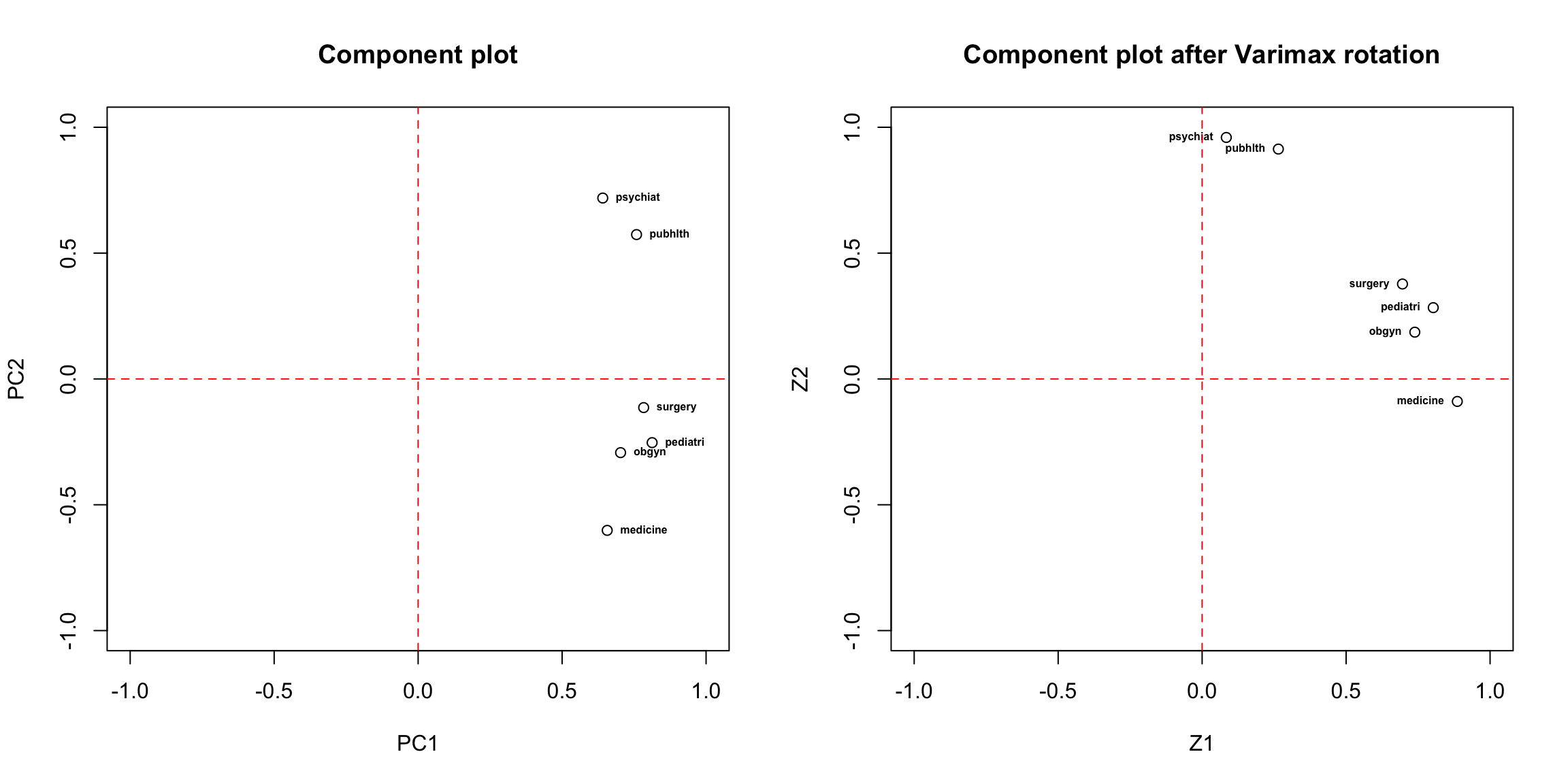
Oblimin rotation
By default, the psych package does not do Kaiser
normalization as SPSS does. To request Kaiser normalization, we can
specify normalize = T.
(med.pca.oblm <- principal(med.data, nfactors = 2, rotate = "oblimin")) ## Principal Components Analysis
## Call: principal(r = med.data, nfactors = 2, rotate = "oblimin")
## Standardized loadings (pattern matrix) based upon correlation matrix
## TC1 TC2 h2 u2 com
## medicine 0.93 -0.21 0.79 0.207 1.1
## psychiat -0.07 0.98 0.93 0.072 1.0
## obgyn 0.73 0.09 0.58 0.420 1.0
## pediatri 0.78 0.18 0.72 0.276 1.1
## pubhlth 0.12 0.91 0.90 0.096 1.0
## surgery 0.65 0.29 0.63 0.374 1.4
##
## TC1 TC2
## SS loadings 2.52 2.03
## Proportion Var 0.42 0.34
## Cumulative Var 0.42 0.76
## Proportion Explained 0.55 0.45
## Cumulative Proportion 0.55 1.00
##
## With component correlations of
## TC1 TC2
## TC1 1.00 0.29
## TC2 0.29 1.00
##
## Mean item complexity = 1.1
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.08
## with the empirical chi square 10.46 with prob < 0.033
##
## Fit based upon off diagonal values = 0.97med.pca.oblm$communality #communality## medicine psychiat obgyn pediatri pubhlth surgery
## 0.7933364 0.9277259 0.5801000 0.7244654 0.9043401 0.6264004med.pca.oblm$loadings #loadings (pattern matrix)##
## Loadings:
## TC1 TC2
## medicine 0.929 -0.215
## psychiat 0.982
## obgyn 0.731
## pediatri 0.780 0.183
## pubhlth 0.121 0.909
## surgery 0.654 0.295
##
## TC1 TC2
## SS loadings 2.453 1.965
## Proportion Var 0.409 0.327
## Cumulative Var 0.409 0.736med.pca.oblm$Structure #correlations structure matrix## TC1 TC2
## medicine 0.8666711 0.05303419
## psychiat 0.2096111 0.96062138
## obgyn 0.7566729 0.30126406
## pediatri 0.8329763 0.40762285
## pubhlth 0.3828357 0.94390320
## surgery 0.7394213 0.48336870med.pca.oblm$Phi #component correlation## TC1 TC2
## TC1 1.0000000 0.2882117
## TC2 0.2882117 1.0000000med.pca.oblm$weights #component score coefficients## TC1 TC2
## medicine 0.393943359 -0.157400417
## psychiat -0.079816607 0.509435468
## obgyn 0.296842658 0.009857899
## pediatri 0.312740127 0.054742162
## pubhlth 0.003969024 0.462194564
## surgery 0.255164066 0.118795623med.pca.oblm$Vaccounted #var explained## TC1 TC2
## SS loadings 2.5222828 2.0340853
## Proportion Var 0.4203805 0.3390142
## Cumulative Var 0.4203805 0.7593947
## Proportion Explained 0.5535731 0.4464269
## Cumulative Proportion 0.5535731 1.0000000med.pca.oblm$scores #PC scores## TC1 TC2
## [1,] 0.8992677788 0.56598355
## [2,] 0.8718929656 0.85152262
## [3,] 2.4872490086 1.81150583
## [4,] 0.2227396264 0.01084618
## [5,] -0.2322086031 -0.62194283
## [6,] 0.8166833001 -1.12456486
## [7,] 1.5334694829 -0.79287378
## [8,] -0.6124431821 0.14823519
## [9,] -1.2329226296 -1.04217330
## [10,] 0.1251422163 -1.01386583
## [11,] -0.3875947273 -0.41104845
## [12,] -0.4153610350 -0.71153251
## [13,] -0.4785571476 0.05153553
## [14,] 0.0004911595 0.09866482
## [15,] 0.7227718643 1.10592588
## [16,] 0.4211794073 0.86418281
## [17,] -0.3365583344 0.22616147
## [18,] 0.3046850291 1.20044497
## [19,] -0.8676757059 -0.57843277
## [20,] 0.8850566819 0.74223447
## [21,] 1.1364415616 0.27889104
## [22,] 0.6534152928 -0.75384203
## [23,] 1.2162170307 0.46832297
## [24,] 0.4337227127 -0.49917881
## [25,] 0.0936429467 0.61108252
## [26,] -0.9595068644 0.93927696
## [27,] 0.1178925501 0.56192329
## [28,] 0.1866141330 1.69002591
## [29,] 1.0468122164 0.45082978
## [30,] -1.0059365363 0.19890672
## [31,] -0.9224662940 -0.23144273
## [32,] -0.1585896550 -0.42470366
## [33,] -0.2029216619 -0.54108716
## [34,] -2.5255155530 -0.08370114
## [35,] 2.6782089263 0.04111394
## [36,] -1.4630175325 1.34920035
## [37,] 1.3036147594 0.93440547
## [38,] -0.6214891401 1.82638047
## [39,] 0.5132366238 0.50606304
## [40,] -0.3007657098 0.91936727
## [41,] -2.1166858620 -1.98106950
## [42,] 0.4038033670 0.20653216
## [43,] -0.7212950597 -1.22704670
## [44,] -0.3589044514 -0.45090998
## [45,] -1.3306574028 -0.57085497
## [46,] 0.9166157606 1.08706686
## [47,] 0.1149616226 0.19302020
## [48,] -0.1778974050 0.38948185
## [49,] -0.7591234599 -0.93972011
## [50,] 0.4139671613 0.40636223
## [51,] 0.2430740599 -0.18338367
## [52,] 1.2123678976 0.70613811
## [53,] 0.2181179567 1.38841865
## [54,] -0.4717756086 -1.49798361
## [55,] -2.0841423246 0.52840096
## [56,] -1.2217386511 -1.41917832
## [57,] 0.4092185777 -0.02959027
## [58,] 0.4092185777 -0.02959027
## [59,] -1.4022692607 -0.83067234
## [60,] 0.2111452918 -1.62274349
## [61,] 0.1450822510 -3.74532093Let’s see how the components look differently than they were before
rotation:
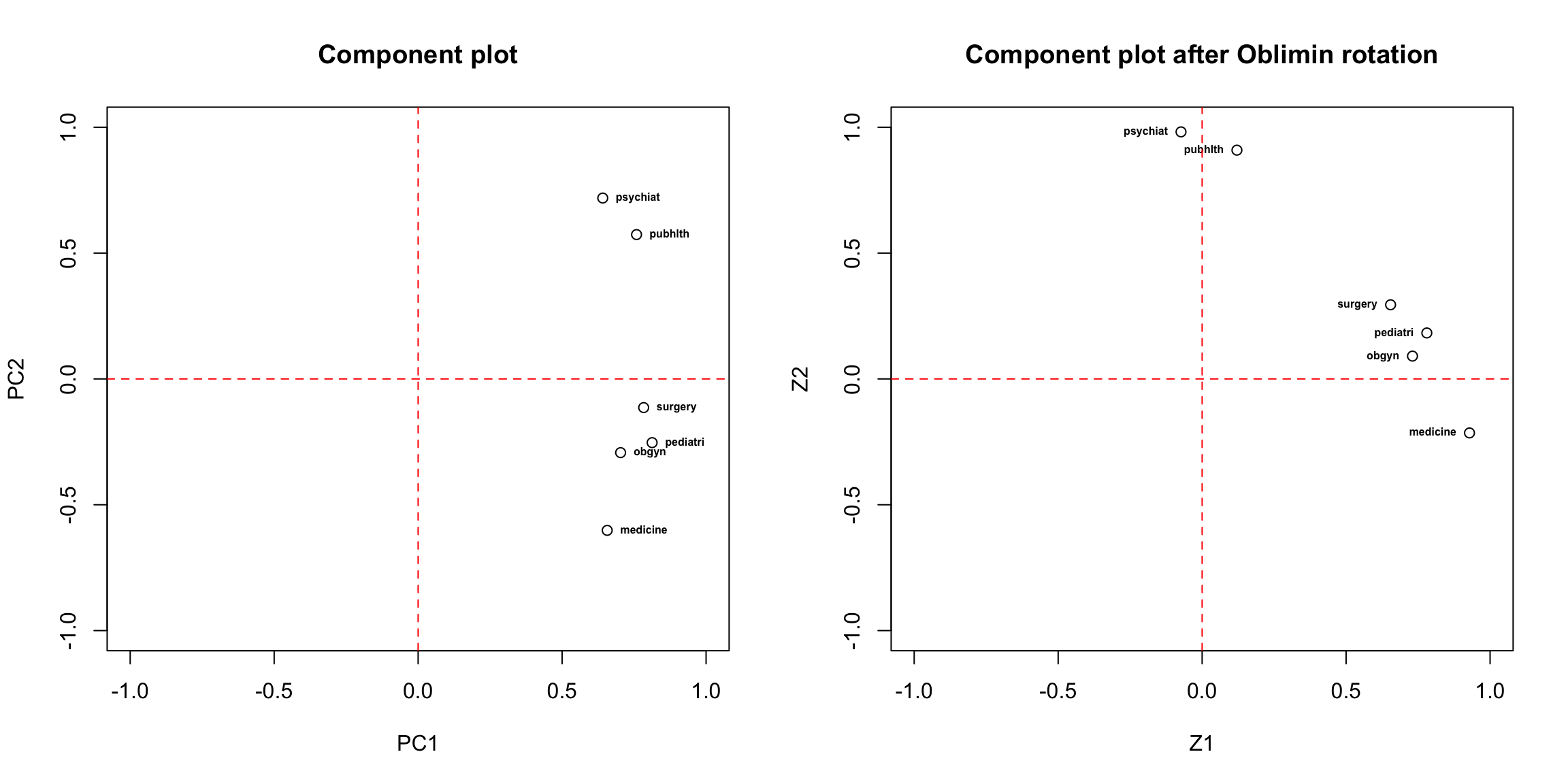
We can still use the factor.model function to compute
the reproduced correlation matrix with oblique rotation, by adding the
factor correlation matrix to the input.
rep.cor <- factor.model(med.pca.oblm$loadings, Phi = med.pca.oblm$Phi)
# residuals
(rep.res <- med.cor - rep.cor)## medicine psychiat obgyn pediatri pubhlth
## medicine 0.20666364 0.046198110 -0.1565865912 -0.053199841 0.0439895296
## psychiat 0.04619811 0.072274127 -0.0178810971 0.002633882 -0.0560787028
## obgyn -0.15658659 -0.017881097 0.4199000063 -0.109692940 0.0007213988
## pediatri -0.05319984 0.002633882 -0.1096929398 0.275534574 -0.0187119126
## pubhlth 0.04398953 -0.056078703 0.0007213988 -0.018711913 0.0956599298
## surgery -0.05793012 -0.030270851 -0.1178954174 -0.126847618 -0.0648494424
## surgery
## medicine -0.05793012
## psychiat -0.03027085
## obgyn -0.11789542
## pediatri -0.12684762
## pubhlth -0.06484944
## surgery 0.37359957Alternatively, you may choose to compute the reproduced correlation matrix using matrix algebra.
\[\hat{\mathbf{\Sigma}} = \mathbf{L}\mathbf{\Phi}\mathbf{L}^{'}\]
rep.cor2 <- med.pca.oblm$loadings %*% med.pca.oblm$Phi %*% t(med.pca.oblm$loadings)
(rep.res2 <- med.cor - rep.cor2)## medicine psychiat obgyn pediatri pubhlth
## medicine 0.20666364 0.046198110 -0.1565865912 -0.053199841 0.0439895296
## psychiat 0.04619811 0.072274127 -0.0178810971 0.002633882 -0.0560787028
## obgyn -0.15658659 -0.017881097 0.4199000063 -0.109692940 0.0007213988
## pediatri -0.05319984 0.002633882 -0.1096929398 0.275534574 -0.0187119126
## pubhlth 0.04398953 -0.056078703 0.0007213988 -0.018711913 0.0956599298
## surgery -0.05793012 -0.030270851 -0.1178954174 -0.126847618 -0.0648494424
## surgery
## medicine -0.05793012
## psychiat -0.03027085
## obgyn -0.11789542
## pediatri -0.12684762
## pubhlth -0.06484944
## surgery 0.37359957Note that unlike SPSS, $Vaccounted prints the correct
value for variance explained, by takes into account the fact that the
principal components are non-orthogonal. It is computed by finding the
diagonal of the following matrix:
\[ (\Sigma_{structure})^TL_{loading} \]
Promax rotation
(med.pca.pro <- principal(med.data, nfactors = 2, rotate = "promax")) ## Principal Components Analysis
## Call: principal(r = med.data, nfactors = 2, rotate = "promax")
## Standardized loadings (pattern matrix) based upon correlation matrix
## RC1 RC2 h2 u2 com
## medicine 0.97 -0.29 0.79 0.207 1.2
## psychiat -0.16 1.02 0.93 0.072 1.0
## obgyn 0.75 0.04 0.58 0.420 1.0
## pediatri 0.79 0.13 0.72 0.276 1.1
## pubhlth 0.05 0.93 0.90 0.096 1.0
## surgery 0.65 0.25 0.63 0.374 1.3
##
## RC1 RC2
## SS loadings 2.53 2.02
## Proportion Var 0.42 0.34
## Cumulative Var 0.42 0.76
## Proportion Explained 0.56 0.44
## Cumulative Proportion 0.56 1.00
##
## With component correlations of
## RC1 RC2
## RC1 1.00 0.42
## RC2 0.42 1.00
##
## Mean item complexity = 1.1
## Test of the hypothesis that 2 components are sufficient.
##
## The root mean square of the residuals (RMSR) is 0.08
## with the empirical chi square 10.46 with prob < 0.033
##
## Fit based upon off diagonal values = 0.97med.pca.pro$Vaccounted## RC1 RC2
## SS loadings 2.5332441 2.0231241
## Proportion Var 0.4222073 0.3371873
## Cumulative Var 0.4222073 0.7593947
## Proportion Explained 0.5559788 0.4440212
## Cumulative Proportion 0.5559788 1.0000000med.pca.pro$communality## medicine psychiat obgyn pediatri pubhlth surgery
## 0.7933364 0.9277259 0.5801000 0.7244654 0.9043401 0.6264004med.pca.pro$loadings##
## Loadings:
## RC1 RC2
## medicine 0.974 -0.294
## psychiat -0.156 1.019
## obgyn 0.746
## pediatri 0.789 0.127
## pubhlth 0.929
## surgery 0.650 0.253
##
## RC1 RC2
## SS loadings 2.578 2.068
## Proportion Var 0.430 0.345
## Cumulative Var 0.430 0.774The R script for this tutorial can be found here.
© Copyright 2022 Yi Feng and Gregory R. Hancock.